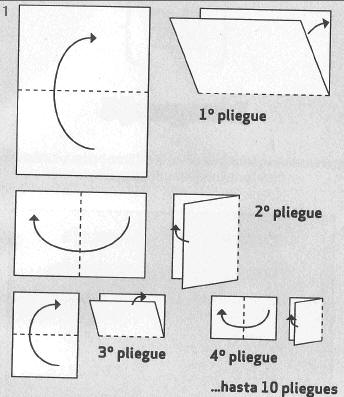
Supongamos que tiene un papel del tamaño de una hoja de periódico y con un espesor de 0,1 mm., o sea 1 décima de milímetro, propia del fino papel Biblia. ¿Cuántas veces cree que podrá doblarlo por la mitad? ¿Cinco, diez, veinte?,...inténtelo. ¿Ha logrado hacer el décimo pliegue? Felicidades, es usted un fortachón, porque ha conseguido doblar un grosor de papel de 10,24 cm, más ancho que el lomo de cualquier enciclopedia.

Cada vez que doblamos el papel por la mitad, duplicamos su grosor en progresión geométrica. Imagínese llegar al vigésimo pliegue, significaría que había conseguido una doblez de 104,86 m de altura.

Un elemento para la reflexión: cada vez que doblamos el papel es más evidente que pasamos de una situación en la que empezamos con un objeto plano, prácticamente de sólo dos dimensiones (anchura x longitud), a un objeto en tres dimensiones. O sea, que sin modificar el material, hemos alterado, mediante la simple duplicación, su representación en el espacio; en definitiva, un modo diferente de ver el mismo objeto.

Imagine un cubo de 1 cm. de lado, su volumen será: 1 x 1 x 1= 1cm3, ahora duplique el lado, osea vale 2, entonces ¿cuánto valdrá ahora el volumen?. Calculando es 2 x 2 x 2 = 8 cm3, es decir, que duplicando el lado de un cubo su volumen se octuplica. Muchas veces vemos una botella no mas grande que otra de medio litro, y resulta que su volumen es 2 litros, bien es consecuencia de los que acabamos de comprobar.

Respecto al doblado de un papel , el divulgador científico Leonardo Moledo, dice:

"....Es difícil imaginarse con qué pasmosa velocidad aumentaría el espesor de papel silo siguiéramos doblando y doblando: con sólo 20 dobleces llegaría a tener cincuenta metros. Pero eso no es nada: con 28 dobleces superaría los 8800 metros de altura del monte Everest y con 38 dobleces los doce mil kilómetros que mide el diámetro de la Tierra. Y eso tampoco es nada: si seguimos doblando el papel, después de 43 dobleces el espesor superaría los 380 mil kilómetros que nos separan de la Luna, y después de 52 dobleces, los ciento cincuenta millones de kilómetros que nos separan del Sol.

Pero aun así, no estamos más que al principio: después de haberlo doblado 58 veces, el espesor del papel será superior al ancho del sistema solar (que es aproximadamente doce mil millones de kilómetros) y con 70 dobleces llegaría más allá de Alfa Centauro, que es la estrella más cercana a la Tierra y que se encuentra a 4 años luz (un año luz, la distancia que la luz recorre en un año, equivale a diez millones de millones de kilómetros). Con 86 dobleces el papel sería más ancho que nuestra galaxia y con 90 dobleces alcanzaría Andrómeda, la galaxia más cercana a la Tierra y que se encuentra a dos millones de años luz. Con 100 dobleces, se encontraría a mitad de camino de los objetos más lejanos observados en el universo, a diez mil millones de años luz, y con un doblez más, sería más ancho que todo el universo conocido.

Estos sorprendentes resultados se deben al rápido crecimiento de las progresiones geométricas (1, 2, 4, 8, 16, 32, etc.), que aumentan a una velocidad pasmosa y anti-intuitiva: hay una leyenda que vincula este fenómeno al origen del ajedrez. Según esta leyenda, cuando Sissa, el inventor hindú del gran juego, se lo presentó al rey y éste le preguntó qué quería como recompensa, Sissa pidió “algo muy simple: un grano de trigo en la primera casilla, dos en la segunda, cuatro en la tercera, ocho en la cuarta y así siguiendo hasta completar el tablero”. El rey se asombró por la modestia de Sissa, accedió inmediatamente, ordenó que trajeran un poco de trigo y se empezara a llenar las casillas."

Explicación de la Leyenda del juego de ajedrez
No se ha podido determinar el origen del juego de ajedrez. Se sabe que fue introducido en Occidente por los árabes, quienes lo habían aprendido de los persas. El califa Harún al-Rashid le regaló uno de marfil a Carlomagno. Ideado por un pueblo guerrero, dio pie a la anécdota que sigue.

Se atribuye su invención al brahmán hindú Sissan ben Daher, que presentó el juego al rey Shirham. Éste, embelesado, quiso compensar al brahmán y le pidió que formulara un deseo. Sissan le respondió que le bastaría con un grano de trigo para la primera casilla, 2 granos para la segunda casilla, 4 granos para la tercera y así sucesivamente, doblando la cantidad hasta la casilla 64 del tablero. Al monarca le sorprendió la modestia de semejante petición y dio la orden de satisfacerla. «Imposible —le respondió su ministro tras haber efectuado los cálculos correspondientes— ¡habría que sembrar toda la Tierra de trigo y esperar la cosecha de varios años!»

El soberano ignoraba el alcance de una progresión geométrica de razón 2 hasta 2⁶³: colocando en la la 1° casilla  1 grano de trigo; en la 2° casilla 2 granos (2¹), en la 3° casilla 4 granos (2²), en la 4° casilla 8 granos (2³), en la 5° casilla 16 (2⁴) granos, y al hasta la casilla 64°, donde  habría que colocar 2⁶³ granos. Este total representaría:

2⁶³ = 18.446.744.073.709.551.614 granos, lo que equivale a unos 9.557.898.400.000 m3 de trigo.

Si hubiera que almacenar toda esta cantidad de trigo, haría falta un silo de 5 m de altura, 8 m de ancho y 238.947.460 Km. de largo. Una alternativa sería ir suministrando al audaz inventor del juego la cosecha entera de todo el mundo durante más de 5.000 años.

Los llamados «juegos en cadena» se basan en el mismo principio y son simples engañabobos. Utilizados como sistemas de venta, conocidos también como «la pirámide», han sido prohibidos en varios países por tratarse de un timo.

Consisten en ofrecer al público una mercancía a un precio muy módico para conseguir el reembolso y un beneficio sustancial a base de colocar bonos a 4, 6 u 8 nuevos clientes llamados «ahijados». La interrupción de la cadena es inevitable: en el escalón 13 de 6 nuevos ahijados, habría más poseedores de bonos (13.060.694.016) que habitantes en la Tierra.

Arte Japonés: Figuras Con Papel Plegado