|
Los Cuadrado Mágicos
Introducción Histórica: Como dirían muchos historiadores, los
orígenes de los cuadrados mágicos se pierden en la oscuridad de los
tiempos pasados, pero sabemos que los sacerdotes egipcios los empleaban para
predecir el futuro, y en China, en el año 2200 a C. el emperador Shu vio
el cuadrado mágico de 3x3 en el caparazón de una tortuga en el río Lo. . También
los indios, los egipcios, los árabes y los griegos tuvieron constancia de su
existencia. En todas estas civilizaciones generalmente se le atribuían a estos
cuadrados propiedades místicas.
Los
mas antiguos escritos que llegaron hasta nuestra manos en la actualidad son del
siglo VIII, de origen árabe, pero aparentemente el autor fue un pensador de la
escuela de Alejandría, conocido como Apolonio de Tiana, y se supone que la
entrada a Europa fue a través del matemático bizantino Moschopoulos, que
estudio varias de sus propiedades y resolvió varios cuadrados de diversos
ordenes. Sus curiosas e interesantes características atrajeron la atención de
muchos matemáticos importantes como , Pascal, Leibnitz, Euler, que en los siglos
XVI y XVII se ocuparon con gran interés.
 La
Leyenda China de Lo-Shu: 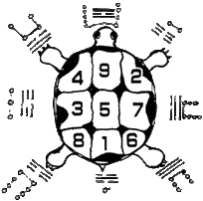El relato
cuenta que estando el emperador Shu, contemplando el río Lo (actual Amarillo)
para intentar encontrar una solución a los problemas creados en la agricultura
por las seguidas crecidas o desbordamiento del mismo, emerge una tortuga
gigante, símbolo del conocimiento y longevidad, y en su caparazón tenía grabado
un diseño de puntos coloreados que formaban un cuadrado. Dichos puntos formaban
nueve números, cada uno de los cuales se inscribía en un pequeño cuadrado, que a
su vez estaba integrado en el cuadrado completo del caparazón, en una
disposición de tres sectores por tres.
Lo
curioso del caso es que los números sumaban un total de quince leyéndolos
en cualquier sentido, horizontal, vertical o diagonal. Los números y su
disposición en el caparazón de la tortuga fueron estudiados por los sabios del
momento y se trasladaron a un cuadrado que se denominó el cuadrado lo shu o
cuadrado mágico que se convirtió en la base de la numerología china, la
astrología, el I Ching y el Feng-shui.
Cuadrados Mágicos: el mundo de los cuadrados
mágicos es muy interesante y apasiona a todos los que tenemos cierta inclinación
por lo números. Mas allá de una curiosidad matemática, se presenta también como
un desafío para conseguir resolver esta especie de rompecabezas matemático,
obligándonos a pensar y a la vez nos ayuda a desarrollar nuestra capacidad de
razonamiento y abstracción. Muchos profesores y especialista lo recomiendan en
las escuelas y hogares como ejercicios diarios para chicos y también para
adultos, sobretodo aquellos que están en etapas mas sedentarias de sus vidas en
donde las exigencias son menores.
Ahora
bien, que es un Cuadrado Mágico?,....es una
cuadrilla o cuadricula de forma cuadrada, y como tal está dividida en celda
cuadradas menores, es decir es una grilla de n
celdas verticales por n celdas horizontales, en
donde a n se le llama Grado del Cuadrado. El
cuadrado de aquí abajo tiene grado 4 porque posee 4 celdas verticales por 4
celdas horizontales.
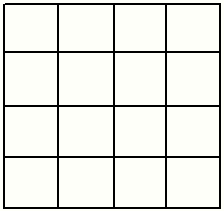
Cuadrado de 4 celdas verticales
por 4 horizontales
Posee 16 celdas en total, el grado es 4
Para
convertir a esta grilla en un cuadrado mágico, debemos colocar adentro de cada
celda un numero natural entre el 1 y el 9 sin repetir, de tal manera que la suma de los
mismo en forma vertical y horizontal sea siempre igual, a dicho valor se lo
conoce como constante mágica del cuadrado.
El
valor de la constantes se puede obtener con la siguiente fórmula: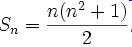
Por
ejemplo para el grado n=3, la suma deber ser igual:
Sn=3.(32 + 1)/2= 15
Y así se puede calcular para cada
orden del cuadrado, por ejemplo si n=4, Sn será 34
Como
curiosidad si usamos una grilla de n=2, es imposible conseguir un cuadrado
mágico, y se puede demostrar armando un sistema de ecuaciones y
concluyendo que en realidad no hay 4 números distintos que sumandos en sentido
vertical y horizontal no dé 5.
Normalmente el desafío para los curiosos es el de armar un cuadrado mágico con
el propio esfuerzo, mediante el sentido común e ir probando hasta conseguir el
resultado buscado, y como decíamos antes es muy utilizado para "mover" un poco
mas nuestras neuronas, y desarrollar nuestra mente. Pero a los fines prácticos
hay varios métodos probados para hacer cuadrado mágicos sin pensar , con solo
repetir una serie de pasos mecanizados. A continuación se presentan dos métodos,
uno para cuadrados mágicos de orden par, donde n es 2,4,6,8...etc., y
otro para cuadrados de orden impar.
Resolución de Cuadrados Mágicos de
Orden Impar por el Método de Loubere:
Ejemplo: Cuadrado Mágico de orden 5, aplicando la formula se tiene que la
constante mágica es igual a 65.
Se
coloca el número 1 en la posición central de
la fila superior y vamos rellenando en diagonal hacia
arriba y a la derecha, es decir, el 2 se coloca en la posición (5,4)
(fila 5, columna 4), el 3 en la posición (4,5), el 4 en la (3,1), y así
sucesivamente.
Cuando al intentar colocar un número en la posición que debe ocupar nos la
encontramos ya ocupada colocamos ese número justo
debajo del último que hemos colocado y continuamos colocando en
diagonal.
El
cuadrado mágico de orden 5 obtenido con este procedimiento es el siguiente:
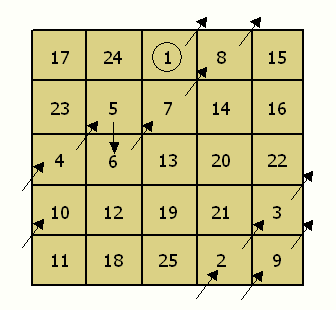
Resolución de Cuadrados Mágicos de
Orden Par, pero que sea múltiplo de 4 (Método 4k)
Ejemplo: Resolución Cuadrado Mágico de Orden 4 (mas chico de los pares)
Inicialmente llenamos el cuadrado con los números
naturales en forma correlativa comenzando desde el 1 en la celda superior
izquierda y avanzando hacia la derecha y hacia abajo (es mas fácil ver la figura
de abajo que explicar este paso)
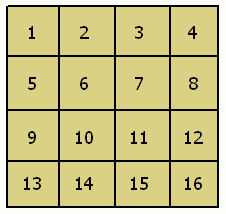
Hacemos las dos diagonales como indica la figura siguiente
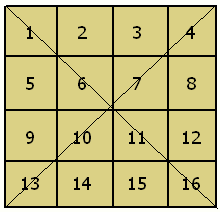
Entonces los números que quedan afuera de las diagonales, que son el
2,3,5,8,9,12,14,15 no se mueve y quedan donde están, y los otros que son
cortados por ambas diagonales se invierten de posición POR
SU SIMÉTRICO. Analizar la figura de abajo, donde está el cuadrado
resuelto, observar como el 1 pasa donde está el 16 y viceversa. Igual para
el 4 con el 13, el 10 con el 7 y 6 con el 11.
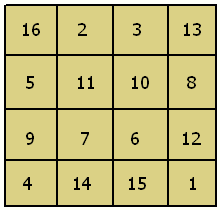
Si el orden de cuadrado es 8,16,24,...etc., a la
grilla se la debe dividir en cuadrados mas chicos de 4 celdas cada uno, y
efectuar este mismo método estudiando a todo el cuadrado grande. Solo hay que
observar bien y ver cual es el simétrico de los números que son cortados por las
diagonales.
Por ejemplo para el de grado 8
se tiene, que el simétrico del 1 es el 64, de 8 es el 57, para el 4 el simétrico
es el 61, para el 5 el simétrico es 60, para el 10 es el 55, para el 11 es el
54, para el 18 es el 47, para el 19 el 46, y así sucesivamente se van
invirtiendo todos los números.
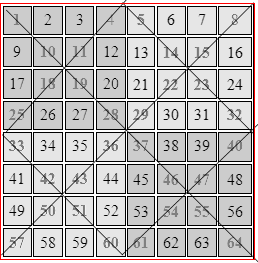
El
error en la solución de estos problemas es cuando uno
determina el simétrico, es muy común que se equivoquen al buscarlo en la
grilla,
pero el método es sí es sumamente fácil y práctico.
Matemáticamente para determinar el simétrico en la se calcula con la formula:
(n+1)-nf ó (n+1)-nc
Por ejemplo el 50 tiene coordenadas: fila nf=7 y columna nc=2 entonces
aplicando la formula se obtienen
las coordenadas del simétrico es: fila=(8+1)-7=2 y columna=(8+1)-2=7, ósea es
el: 15
El
noble Claude Gaspard Bachet de Méziriac (1581-1638) consideró que los
cuadrados mágicos constituían sólo una parte lúdica de las matemáticas y, en
1612, publicó un libro con un título muy sugerente: Problemas agradables y
deleitosos que se hacen con números, muy útil para toda clase de personas
curiosas que saben algo de aritmética. Aunque él se preciaba de haber inventado
fórmulas nuevas para la construcción de cuadrados mágicos, esto no fue realmente
así y ya su contemporáneo Pierre
Fermat le acusó de plagio.
Respecto a las reglas para armar estos rompecabezas matemáticos podemos decir
que hay infinitas variantes para establecer una forma de distribuir los números
en cuadrillas de celdas. Prácticamente es cuestión de plantear una
forma de reparto y luego empezar a pensar como se puede cumplir con dicho
planteo. También se suelen usar números negativos, pueden ser también letras o
colores, pero bueno son todas extensiones de estos primeros maravillosos
cuadrados mágicos que han sorprendido y apasionados a miles de matemáticos (y no
matemáticos) de la historia.
A
modo de ejemplo, se plantea el siguiente ejercicio:
Distribuir los números 1,2,3,4,6,9,12,18 y 36 de tal manera que al multiplicar
cualquier linea vertical, horizontal o diagonal, el resultado siempre sea el
mismo, te animas?
|
