En su Studio (Real Academia de Venecia), también conocido como El hombre de
Vitruvio, Leonardo da Vinci realiza una visión del hombre como centro del
Universo al quedar inscrito en un círculo y un cuadrado. El cuadrado es la base
de lo clásico: el módulo del cuadrado se emplea en toda la arquitectura clásica,
el uso del ángulo de 90º y la simetría son bases grecolatinas de la
arquitectura. En él se realiza un estudio anatómico buscando la proporcionalidad
del cuerpo humano, el canon clásico o ideal de belleza.
Sigue los estudios del
arquitecto Vitruvio (Marcus Vitruvius Pollio) arquitecto romano del siglo I
a.c. a quien Julio Cesar encarga la construcción de máquinas de guerra. En época
de Augusto escribió los diez tomos de su obra
De architectura, que trata de la
construcción hidráulica, de cuadrantes solares, de mecánica y de sus
aplicaciones en arquitectura civil e ingeniería militar. Vitrubio tuvo escasa
influencia en su época pero no así en el renacimiento ya que fue el punto de
partida de sus intentos y la justificación de sus teorías.
Su obra fue publicada
en Roma en 1486 realizándose numerosas ediciones como la de Fra Giocondo en
1511, Venecia o la de Cesare Cesarino en 1521, Milán, dedicada a Francisco I.
Parece indudable que Leonardo se inspiró en el arquitecto romano.
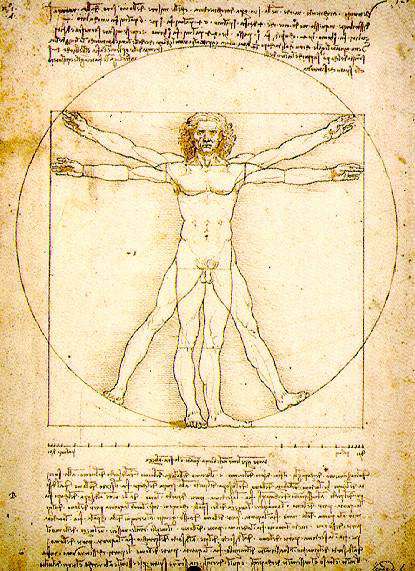
La
Proporciones del Hombre de Vitruvio
“Vitrubio el arquitecto, dice en su obra sobre
arquitectura que la naturaleza distribuye las medidas del cuerpo humano como
sigue: que 4 dedos hacen 1 palma, y 4 palmas hacen 1 pie, 6 palmas hacen 1 codo,
4 codos hacen la altura del hombre. Y 4 codos hacen 1 paso, y que 24 palmas
hacen un hombre; y estas medidas son
las que él usaba en sus edilicios. Si separas la piernas lo suficiente
como para que tu altura disminuya 1/14 y estiras y subes los hombros hasta que
los dedos estén al nivel del borde
superior de tu cabeza, has de saber que el centro geométrico de tus extremidades
separadas estará situado en tu ombligo y que el espacio entre las piernas
será un
triángulo equilátero. La longitud de los brazos extendidos de un hombre es igual
a su altura. Desde el nacimiento del pelo hasta la punta de la barbilla es la
décima parte de la altura de un hombre; desde la punta de la barbilla a la parte
superior de la cabeza es un octavo de su estatura; desde la parte superior del
pecho al extremo de su cabeza será un sexto de un hombre. Desde la parte
superior del pecho al nacimiento del pelo será la séptima parte del hombre
completo. Desde los pezones a la parte de arriba de la cabeza será la cuarta
parte del hombre. La anchura mayor de los hombros contiene en sí misma la cuarta
parte de un hombre. Desde el codo a la punta de la mano será
la quinta parte del hombre; y desde el codo al ángulo de la axila será la octava
parte del hombre. La mano completa será la décima parte del hombre; el comienzo
de los genitales marca la mitad del hombre. El pie es la séptima parte del
hombre. Desde la planta del pie hasta debajo de la rodilla será la cuarta parte
del hombre. Desde debajo de la rodilla al comienzo de los genitales será la
cuarta parte del hombre. La distancia desde la parte inferior de la barbilla a
la nariz y desde el nacimiento del pelo a las cejas es, en cada caso, la misma,
y, como la oreja, una tercera parte del rostro».
La anterior es la traducción completa del texto que
acompaña al Hombre de Vitruvio de Leonardo da Vinci. En realidad es una
traducción de las palabras de Vitrubio pues el dibujo de Leonardo fue
originalmente una ilustración para un libro sobre las obras de Vitrubio. El
Hombre de Vitruvio es probablemente una de las imágenes más famosas y
reconocibles de Leonardo. (En El Código Da Vinci es también la obra de
Da Vinci favorita de Sophie Neveu y es asimismo la postura en la que su abuelo.
Jacques Sauniére. colocó su cuerpo antes de morir).
Carteles con la imagen del hombre con dos pares de
brazos extendidos y dos pares de piernas también extendidas han adornado muchas
paredes durante al menos un par de generaciones. Vitruvio fue un escritor,
ingeniero y arquitecto romano de finales del siglo 1 a. de C. y principios del
siglo 1 de nuestra era. Su único libro existente, De Architectura, contiene diez
enormes capítulos enciclopédicos en los cuales trata distintos aspectos de la
planificación, ingeniería y arquitectura de la ciudad romana, pero también una
sección acerca de las proporciones humanas. Su redescubrimiento y su renovado
auge durante el Renacimiento alimentaron el crecimiento del clasicismo durante
aquel periodo, e incluso en los posteriores.
La composición del Hombre de Vitruvio, tal y como fue ilustrada por Leonardo da
Vinci, se basa por entero en el tratado del propio Vitruvio citado anteriormente
sobre las dimensiones del cuerpo humano, que ha probado ser en buena parte
conecto. El énfasis se pone, al construir la composición, en la racionalización
de la geometría, por medio de la aplicación de números enteros pequeños.
El
hombre de Vitrubio es un claro ejemplo del enfoque globalizador de Leonardo que
se desarrolló muy rápidamente durante la segunda mitad de la década de 1480.
Trataba de vincular la arquitectura y el cuerpo humano, un aspecto de su
interpretación de la naturaleza y del lugar de la humanidad en el "plan global
de las cosas". En este dibujo representa las proporciones que podían
establecerse en el cuerpo humano (por ejemplo, la proporción áurea). Para
Leonardo, el hombre era el modelo del universo y lo más importante era vincular
lo que descubría en el interior del cuerpo humano con lo que observaba en la
naturaleza.
Durante los últimos siglos, creció el mito
de que los antiguos griegos estaban sujetos a una proporción numérica
específica, esencial para sus ideales de belleza y geometría. Dicha proporción
es conocida con los nombres de razón áurea
ó divina proporción.
Aunque recientes
investigaciones revelan que no hay ninguna prueba que conecte esta proporción
con la estética griega, esta sigue manteniendo un cierto atractivo como modelo
de belleza.
Matemáticamente nace de plantear la siguiente proporcionalidad entre dos
segmentos y que dice así: "Buscar dos segmentos tales que el cociente entre
el segmento mayor y el menor sea igual al cociente que resulta entre la
suma de los dos segmentos y el mayor"
Sean
los segmentos:
A: el mayor y B el menor, entoces planteando la ecuación es:
A/B =(A+B)/A
Cuando se resuelve se llega a una ecuación
de 2do. grado que para obtener la solución hay que aplicar la resolvente
cuadrática.
El valor numérico de esta razón, que se
simboliza normalmente con la letra griega "fi" es:
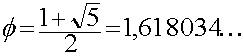
LA SECCIÓN ÁUREA
Los griegos de la antigüedad clásica creían que la
proporción conducía a la salud y a la belleza. En su libro Los Elementos
(300 a. C.), Euclides demostró la proporción que Platón había denominado «la
sección», y que más tarde se conocería como «sección áurea». Ésta
constituía la base en la que se fundaba el arte y la arquitectura griegos; el
diseño del Partenón de Atenas está basado en esta proporción. En la Edad Media,
la sección áurea era considerada de origen divino: se creía que encarnaba la
perfección de la creación divina. Los artistas del Renacimiento la empleaban
como encarnación de la lógica divina. Jan Vermeer (1632-1675) la usó en Holanda;
pero, años después, el interés por ella decreció hasta que, en 1920, Piet
Mondrian (1872-1944) estructuró sus pinturas abstractas según las reglas de la
sección áurea.
También
conocido como la Divina Proporción, la Media Áurea o la Proporción Áurea, este
ratio se encuentra con sorprendente frecuencia en las estructuras naturales así
como en el arte y la arquitectura hechos por el hombre, en los que se considera
agradable la proporción entre longitud y anchura de aproximadamente 1,618. Sus
extrañas propiedades son la causa de que la Sección Áurea haya sido considerada
históricamente como divina en sus composiciones e infinita en sus significados.
Los antiguos griegos, por ejemplo, creyeron que el entendimiento de la
proporción podría ayudar a acercarse a Dios: Dios «estaba» en el número.
Sin duda
alguna. es cierto que la armonía se puede expresar mediante cifras, tanto en
espacios pictóricos o arquitectónicos, como en el reino de la música o, cómo no,
en la naturaleza. La armonía de la Sección Áurea o Divina Proporción se revela
de forma natural en muchos lugares. En el cuerpo humano, los ventrículos del
corazón recuperan su posición de partida en el punto del ciclo rítmico cardiaco
equivalente a la Sección Áurea. El rostro humano incorpora este ratio a sus
proporciones.
Si se divide el grado de inclinación de una espiral de ADN o de la
concha de un molusco por sus respectivos diámetros, se obtiene la Sección Áurea.
Y si se mira la forma en que crecen
las hojas de la rama de una planta, se puede ver que cada una crece en un
ángulo diferente respecto a la de debajo. El ángulo más común entre hojas
sucesivas está directamente relacionado con la Sección Áurea.
En arte y laarquitectura
también se han usado con extraordinarios resultados las famosas propiedades
armoniosas de a Sección Áurea. 1 las dimensiones de la Cámara Real de la Gan
Pirámide se basan en la Sección Áurea; el
arquitecto Le Corhusier diseño su
sistema Modulor basándose en la utilización de la proporción
áurea, el pintor Mondrian
basó la mayoría de
sus obras en la Sección Áurea: Leonardo la incluyó en muchas de
sus pinturas y Claude Dehussy se sirvió de sus
propiedades
en la música. La Sección Áurea también surge en algunos lugares inverosímiles:
los televisores de pantalla ancha, las postales, las tarjetas de crédito y
las fotografías se ajustan por lo común a sus proporciones. Y se han llevado a
cabo muchos experimentos para probar que las proporciones de los rostros de las
top models se adecuan más estrechamente a la Sección Áurea que las del
resto de la población. lo cual supuestamente explica por qué las encontramos
bellas.
Luca Pacioli,
un amigo de Leonardo da Vinci al que conoció mientras trabajaba en la corte de
Ludovico Sforza, duque de Milán, escribió un tratado crucial sobre la Sección
Áurea, titulado De divina proportione. En este libro, Pacioli intenta
explicar el significado de la Divina Proporción de una forma lógica y
científica, aunque lo que él creía era que su esquiva cualidad reflejaba el
misterio de Dios. Esta y otras obras de Pacioli parece que influyeron
profundamente a Leonardo, y ambos se convirtieron en amigos inquebrantables,
trabajando incluso juntos sobre problemas matemáticos. El uso de la Sección
Áurea es evidente en las obras principales de Leonardo, quien mostró durante
mucho tiempo un gran interés por las matemáticas del arte y de la naturaleza.
Como el brillante Pitágoras antes que él, Leonardo hizo un estudio en
profundidad de la figura humana, demostrando que todas las partes fundamentales
guardaban relación con la Sección Áurea. Se ha dicho que la gran pintura
inacabada de Leonardo, San Jerónimo, que muestra al santo con un león a
sus pies, fue pintada en un intencionado estilo para asegurarse de que un
rectángulo dorado (véase entrada) encajara perfectamente alrededor de la figura
central. Dada la afición de Leonardo por la «geometría recreativa», esto parece
una suposición razonable También el rostro de la
Mona Lisa encierra un rectángulo dorado pertecto.
Después de
Leonardo, artistas
como
Ralaei y Miguel ángel hicieron un eran
uso de
la Sección Áurea para construir sus
obras. La
impresionante escultura de Miguel Ángel El David se ajusta en varios
sentidos a la Sección Áurea, desde la situación del ombligo con respecto a la altura, hasta la
colocación de las articulaciones de los dedos.
Los
constructores de las iglesias medievales y góticas y de las catedrales europeas
también erigieron estas asombrosas estructuras para adaptarse a la Sección
Aurea. En este sentido, Dios realmente estaba en los números.
En el suelo
del lugar donde se encuentra el cuerpo de Jacques Sauniére al comienzo del libro
hay escritos algunos números. Sophie, su nieta, reconoce la secuencia numérica y
la interpreta como una señal de su abuelo, aunque lleva su tiempo que emerja su
completa significación. Una vez que ella
tiene
la llave de la caja de depósitos del banco y comprende que necesita un número de cuenta para
tener acceso a ella, las cifras se ordenan
ascendentemente para darle la solución.
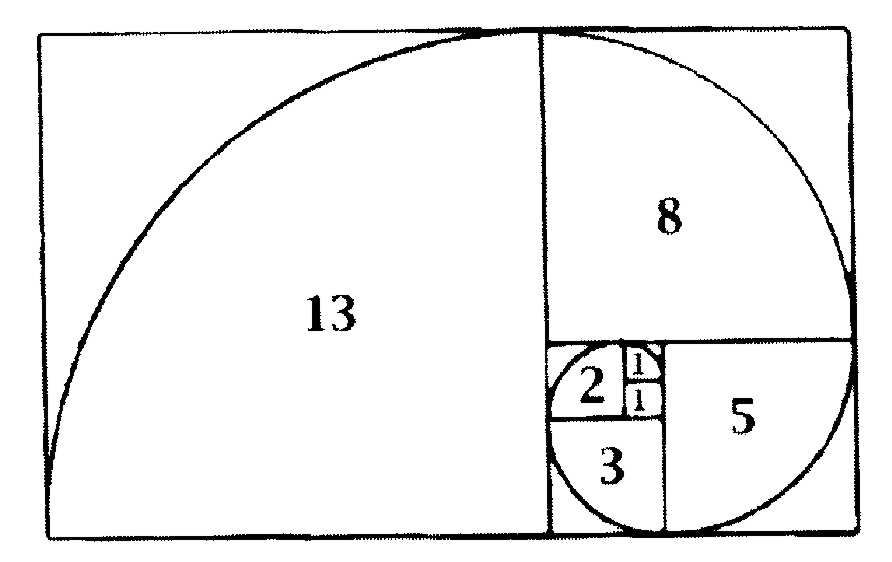
La secuencia
de Fibonacci es una secuencia infinita de número que
comienza por: 1,
1, 2, 3, 5,8,13..., en la que cada
uno de
ellos es la suma de los dos anteriores.
Así: 2=1+1,
3=2+1, 5=3+2, 13=8+5 . Para cualquier valor mayor que 3 contenido en la secuencia, la
proporción entre cualesquiera dos números consecutivos es 1,618, o Sección
Áurea.
La secuencia
de Fibonacci se puede encontrar en la naturaleza, en la que la flor del girasol,
por ejemplo, tiene veintiuna espirales que van en una dirección y treinta y
cuatro que van en la otra; ambos sonnúmeros consecutivos
de Fibonacci. La parte externa de una piña piñonera tiene espirales que van en
sentido de las manecillas del reloj y otras que lo hacen en sentido contrario, y
la proporción entre el número de unas y otras espirales tiene valores
secuenciales de Fibonacci. En las elegantes curvas de una concha de nautilus,
cada nueva circunvolución completa cumplirá una proporción de 1: 1,618, si se
compara con la distancia desde el centro de la espiral precedente.
Leonardo
Fihonacci nació en Pisa. Italia, en 1170. Creció y fue educado en Bugia, norte
de África (hoy llamada Bejaia, en Argelia), desde donde regresó a Pisa alrededor
del año 1200. Fibonacci fue sin duda influido y posiblemente enseñado por
matemáticos árabes durante este su periodo más formativo. Escribió muchos textos
matemáticos e hizo algunos descubrimientos matemáticos significativos, lo que
ayudó a que sus trabajos fueran muy populares en Italia y a que le prestara
atención el Sacro Emperador Romano del momento Federico
II. quien lo invito a su corte de Pisa. Fibonacci murió en 1250.
