Concepto de Inteligencia Artificial:Usos en Robotica y Cibernetica
Concepto de Inteligencia Artificial-Aplicaciones en Robotica y Cibernetica
Los autores de ciencia ficción ya jugaban con la idea de robots humanoides en la década de 1920, antes de la llegada de los ordenadores.
Antes de que existiera la Inteligencia Artificial en 1950, el matemático británico Alan Turing sentó las bases de la robótica al describir una prueba para máquinas inteligentes conocida como test de Turing .
En 1968, la película 2001: Una odisea del espacio mostraba a un ordenador llamado HAL conversando con humanos.
En el mundo real no existía máquina alguna comparable a HAL, si bien dos años antes, el informático de origen alemán Joseph Weizenbaum había creado ELIZA, un programa capaz de convencer a una persona de que estaba hablando con otro ser humano a través de un ordenador, cuando en realidad lo hacía con la propia máquina.
Lo que hacia ELIZA era generar respuestas basadas en palabras clave introducidas por los participantes.
El lenguaje es uno de los aspectos distintivos de la inteligencia humana, y los ordenadores aún no han podido igualar nuestra habilidad con las palabras Sin embargo, hay algo en que lo que son mejores: el procesamiento de datos.
Son capaces de memorizar ingentes cantidades de datos y realizar cálculos que a nosotros nos llevarían años.
Esto los hace excelentes en la resolución de problemas y contrincantes formidables en juegos como el ajedrez.
Las inteligencias emocional y social son difíciles de programar, y estos atributos complejos aún deben ser desarrollados en las máquinas.
Científicos daneses dieron un primer paso en 2000 al construir a Feelix, un robot capaz de transmitir seis emociones -ira, felicidad, tristeza, miedo, sorpresa y una emoción «neutra»- a través de expresiones faciales como respuesta al contacto físico.
Los informáticos han soñado durante largo tiempo con fabricar máquinas capaces de pensar.
Hasta ahora han fracasado, pero durante el proceso nos han enseñado mucho sobre cómo piensan los humanos.
El problema para el ámbito de la inteligencia artificial ha sido definir la inteligencia y demostrar que las máquinas son capaces de tenerla.

En 1996, el ruso Gari Kaspárov, campeón del mundo de ajedrez, jugó seis partidas contra Deep Blue, un ordenador construido por IBM y ganó por 4-2: el hombre triunfó sobre la máquina.
Pero en la revancha jugada un año después Kaspárov perdió por 3,5-2,5 frente a una versión actualizada de Deep Blue: por primera vez, un ordenador derrotaba a un campeón mundial de ajedrez.
Deep Blue ganó porque era capaz de calcular una inmensa cantidad de movimientos en cada jugada y seleccionar el mejor, y porque, a diferencia de Kaspárov, era totalmente inmune a la presión emocional.
------------- 00000 ------------
• CONCEPTO DE LA INTELIGENCIA ARTIFICIAL:
Un Definición Posible: Se puede tomar como defición de Inteligencia Artificial como la capacidad que tienen las máquinas de "ser inteligentes" y reconocer patrones, habilidad que permite desarrollar soluciones que ayudan a resolver los desafíos y problemas de las personas. La Inteligencia Artificial (IA) es capaz de elaborar relaciones lógicas de causalidad, como por ejemplo, “si hacer frío, me abrigo”.
El matemático británico Alan Turing (1912-1954) diseñó un experimento para probar si una máquina manifiesta inteligencia.
En el experimento de Turing, un ser humano dirige el diálogo —a través de una terminal de ordenador— con una máquina y otro ser humano, escondidos detrás de un biombo.
Ambos deben responder a cada pregunta que se les hace.
Turing argumentó que si el que hacía las preguntas no podía decidir cuál de ellos dos era la máquina, esto quería decir que la máquina había demostrado inteligencia.

Los investigadores de inteligencia artificial han tomado dos vías muy distintas para construir máquinas inteligentes.
Algunos han intentado construir máquinas que utilizan los mismos principios que la inteligencia biológica, mientras otros se han basado en muestras de comportamiento inteligente (por ejemplo, el juego del ajedrez o el lenguaje) y han intentado fabricar máquinas que lo copian.
Desde sus orígenes a mediados de la década de los 50, la investigación de la inteligencia artificial ha abordado una amplia gama de desafíos, que incluyen la resolución de problemas, el lenguaje natural
La inteligencia artificial constituye una rama de la informática que, en los últimos tiempos, está adquiriendo creciente importancia.
Su campo de estudio lo constituyen los procedimientos necesarios para elaborar sistemas entre cuyas prestaciones figuren las que, tradicionalmente, se han considerado privativas de la inteligencia humana.
------------- 00000 ------------
Concepto Moderno
El Machine Learning, o ML, se refiere a la habilidad que tienen las máquinas o los programas para entrenar o desarrollar una Inteligencia Artificial capaz de tomar decisiones sin necesidad de programar reglas en detalle.
------------- 00000 ------------
Los objetivos de la inteligencia artificial:
Un ordenador ejecuta las órdenes para procesar datos que le son suministrados sin que disponga de capacidad para desarrollar razonamiento alguno acerca de dicha información.
Frente a ello, la propuesta de la inteligencia artificial consiste en lograr que el procesador se adapte al método de razonamiento y comunicación humanos, para que pueda, no sólo poner en práctica los algoritmos que en él introduce el hombre, sino establecer los suyos propios para resolver problemas.
El ordenador puede calcular el área de un polígono siempre que posea el programa que le proporciona el dato de la medida de uno de sus lados y la fórmula correspondiente para realizar dicha operación; la inteligencia artificial pretende que el procesador sea instruido en los principios de la geometría, para, por sí mismo, resolver la cuestión, a partir de un algoritmo de su propia creación.
En definitiva, la inteligencia artificial explora los mecanismos que convierten al ordenador en una máquina pensante.
La posibilidad de que esta hipótesis llegue a hacerse realidad es rechazada por numerosos expertos informáticos.
En todo caso, se siguen explorando caminos y, día a día, se constatan los progresos.
------------- 00000 ------------
Concepto Moderno
Modelo de Machine Learning: Un modelo se refiere a todos los pasos que son necesarios para que una máquina inteligente llegue a tomar una decisión. Este paso a paso se conforma por funciones matemáticas específicas, las que se interrelacionan como una red.
------------- 00000 ------------
La máquina pensante y los sistemas expertos:
Los primeros intentos de abordar la resolución de problemas (a menudo utilizada como una medida de inteligencia) dio lugar al programa Logic Theorem en la década de los 50.
Como sugiere su nombre, fue capaz de probar teoremas.
Más tarde surgió un nuevo programa más avanzado llamado General Problem Solver, capaz de abordar problemas matemáticos mas complejos.
El fundamento del GPS era que un problemas podía resolverse partiendo del análisis de todas sus soluciones posibles y actuando con sucesivos intentos hasta halla r el camino adecuado.
r el camino adecuado.
La cuestión que inmediatamente se planteó fue que, dada la ignorancia absoluta sobre determinado tema, la búsqueda de salidas requerirla de un tiempo inadmisible.
Evidentemente, la aplicación del GPS a la resolución de problemas reales resultaba imposible.
Poco tiempo después se idearon los primeros sistemas expertos, especializados en determinados ámbitos; el más célebre, el Mycin, fue diseñado en 1974.
Se aplicó al campo médico, concretamente al área de diagnosis, con resultados más que aceptables.
Los sistemas expertos actúan en función de normas que regulan una relación con el usuario; su misión no es sustituir a la persona encargada de realizar determinada tarea, sino tener la posibilidad de operar sobre la base de sus conocimientos en ausencia de ella.
El especialista es, lógicamente, el encargado de instruir al sistema experto, que dispondrá de una base de conocimientos acerca de un tema en cuestión.
Dichos conocimientos adoptan la forma de principios a partir de los cuales el sistema deduce conclusiones, elabora juicios o toma decisiones.
Además de la exigencia de que la respuesta del sistema experto venga dada en un intervalo de tiempo razonable, son también elementos fundamentales la capacidad de indicar el proceso de resolución efectuado y la posibilidad de adquirir conocimientos a partir de la propia experiencia.
En este último caso, el sistema podrá aplicar los resultados obtenidos en situaciones análogas futuras.
Lenguaje:
Una meta más importante de la investigación de la inteligencia artificial es dar a los seres humanos la posibilidad de interactuar con ordenadores utilizando lenguaje natural, el escrito y hablado por los seres humanos, tan distinto de los lenguajes de programas de ordenador.
Para comprender e interpretar un lenguaje como éste, se necesita mucho más conocimiento de lo que se pudiera pensar.
Los ordenadores tienen que ser capaces de adivinar el contexto en el que se dice una palabra para poder interpretar lo que se dice.
Para este fin, los investigadores de la inteligencia artificial han utilizado algunas de las ideas del lingüista Noam Chomsky , quien sugirió que el lenguaje obedece a un conjunto de reglas que pueden expresarse en términos matemáticos.
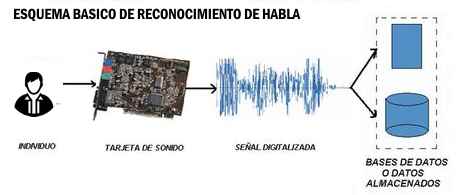
Paralelamente a este trabajo sobre el lenguaje natural, se ha puesto en marcha una investigación sobre el reconocimiento del habla.
Los sistemas de reconocimiento del habla utilizan información sobre la estructura y los componentes del habla y están "preparados" normalmente para la voz de una única persona.
El desafío es desarrollar una máquina que pueda reconocer lo que diga cualquiera de un grupo de hablantes —incluso si su voz se ve afectada, por ejemplo, por un catarro— y distinguir el habla del ruido de fondo.
Los sistemas de reconocimiento del habla: un ingeniero examina un ordenador que habla y escribe, que permite que la máquina interprete y actúe sobre tipos de voz humana.
La interpretación de tipos de voz es un criterio para el desarrollo de sistemas de ordenador de quinta generación en los que la extrema facilidad para el usuario —la habilidad de comunicar en lenguaje natural— sería una de las características más importantes.
Los ordenadores de quinta generación serán radicalmente diferentes de las máquinas existentes y estarán basados en sistemas expertos, lenguajes de programación de muy alto nivel, procesamiento no centralizado y microchips de integración en muy gran escala (VLSI).
------------- 00000 ------------
Las Redes Neuronales:
A mediados del siglo XX nació la teoría de las redes neuronales que parte de una comparación entre el ordenador y el cerebro humano, y cuyo objetivo es imitar el funcionamiento del sistema neuronal.
Podría decirse que el cerebro en el lenguaje informático, sería un sistema paralelo formado por ingentes cantidades de procesadores interconectados entre si: las neuronas.
Siguiendo el proceso de funcionamiento de las neuronas cerebrales los investigadores McCulloch y Pitts idearon en 1943 el modelo que lleva su nombre.
El modelo de McCulloch y Pitts se realiza a partir de una red de gran tamaño, formada por elementos simples cuya misión es el cálculo de sencillas funciones —La neurona únicamente debe realizar la suma ponderada de los impulsos de otras neuronas, un programa básico—.
Sin embargo, habitualmente, un número reducido de calculadores ejecuta programas de enorme complejidad; en el transcurso del proceso, un pequeño error puede repercutir fatalmente en el resultado.
Por otra parte, las neuronas cerebrales se comunican con una velocidad varios millones de veces más lenta que la velocidad de operación de los circuitos electrónicos.
Por el contrario, el cerebro humano procesa determinado tipo de datos, como imágenes o sonidos, mucho más rápidamente que el ordenador.
Almacenar conocimientos:
Los ordenadores son capaces de almacenar una enorme cantidad de información, pero ésta no puede archivarse en una masa sin orden ni concierto; el ordenador necesita llegar a unos específicos bits de información para solucionar un problema concreto.
Para decidir de que forma deberían los ordenadores almacenar información de una manera más eficaz para los fines de la inteligencia artificial, los científicos han explorado de qué modo los seres humanos almacenan y acceden al conocimiento en sus cerebros.
Como resultado aleatorio de esta investigación, se han descubierto un gran número de cosas sobre el aprendizaje de los seres humanos.
Sistemas Expertos:
El resultado mas tángible y práctico de la investigación de la inteligencia artificial han sido los sistemas expertos temas expertos.
Éstos son diseñados para ayudar a los humanos a tomar decisiones, normalmente en la resolución de problemas en los que de otra manera hubiera sido necesario pedir la ayuda de un especialista en un campo específico.
Muchos de los primeros sistemas expertos se dedicaron a simplificar el diagnóstico médico, pero en la actualidad la industria y el comercio han empezado a tomarlos más en serio.
Las compañías financieras los utilizan para aconsejar sobre si a un cliente se le debería conceder un préstamo, o qué tipo de seguro sería más adecuado a sus necesidades.
Los sistemas expertos también han sido ulilizados en la prospección de minerales y análisis de productos químicos, y para la fabricación de ordenadores.
Son particularmente valiosos ahí donde hay que lomar las decisiones cu un ambiente hostil. por ejemplo en las plañías de energía nuclear.
Un sistema experto tiene tres componentes:
1) una base de datos o base de conocimiento, en la que se resumen el conocimiento y la experiencia de un experto en forma de reglas;
2) un motor de inferencia, que es un programa que examina la base de conocimiento para la mejor respuesta posible a una pregunta;
3) un interfaz de usuario, que permite que el usuario hable con el sistema.
El software necesario para fabricar un sistema experto —denominado shell (armazón)— ya está ampliamente disponible.
Sin embargo, aunque a un shell sólo le falte la base de conocimiento, la fabricación de ésta demuestra ser difícil y lenta en la práctica.
Los expertos a menudo encuentran difícil explicar con exactitud a un informático cómo llegan a sus decisiones, y traducir las mecánicas de estas decisiones —que pueden depender en gran parte de la experiencia y de la intuición— a la lógica matemática exacta requerida por un ordenador resulta una tarea ciertamente complicada.
El hecho de crear la base de conocimiento ha dado lugar a un nuevo campo de la ingeniería de conocimiento: el proceso de extraer el conocimiento del especialista humano y traducirlo en una base de datos de reglas.
Los sistemas expertos no son de utilidad allí donde son necesarios la intuición o el sentido común; sólo pueden utilizarse cuando el proceso de toma de decisiones sigue un curso lógico sencillo y perfectamente definido.
Pero los sistemas de este tipo son muy valiosos en las situaciones en las que los especialistas son escasos, o como medida para conservar el conocimiento y transferirlo a otros cuando los individuos se jubilan o cambian de trabajo.
Cómputo Neuronal:
Al tiempo que los neurofisiólogos han empezado a descifrar la estructura del cerebro, los científicos tle ordenador han tomado sus descubrimientos como una base potencial para una arquitectura del ordenador.
El cerebro es esencialmente una compleja red de neuronas interconectadas , y esta interconexión es la clave para la rápida resolución de problemas.
Se ha manejado la idea de fabricar una red neuronal desde principios de la década de los 40, pero solamente desde principios de la de los 80 ha vuelto a despertarse el interés por ello.
En este tiempo, la tecnología informática ha avanzado rápidamente, haciendo más real la perspectiva de construir ordenadores neuronales.
Las redes neuronales ofrecen grandes ventajas sobre los ordenadores convencionales en la búsqueda de problemas similares en grandes bases de datos, o en el almacenamiento y entrada de datos.
Estas están formadas por un gran número de procesadores (nodos) —los puntos en los que se procesa la información— interconectados por canales de información.
Los ordenadores neuronales aprenden mediante ejemplos; no están programados como los ordenadores convencionales, lo que significa que no se les da simplemente una serie de instrucciones sobre lo que deben realizar.
Utilizan el concepto de realimentación —en el que parte del outpul (salida) en cierto sentido es devuelto como input (entrada) para otro proceso, para su autocorrección— a causa de lo cual pueden interactuar con su medio.
También se diferencian de los ordenadores convencionales en que al cambiar las interconexiones entre nodos alteran el comportamiento de la red, haciéndola adecuada para un tipo especial de resolución de problemas.
Actualmente, las redes neuronales encuentran ya aplicación en el mundo comercial.
Las primeras de estas aplicaciones se han dado en el asesoramiento financiero, el reconocimiento de intrusos y la detección de explosivos.
La Robótica:
Otra rama importante de la inteligencia artificial es la robótica.
Sin embargo, la tecnología todavía está en sus inicios: a la idea de un robot inteligente que reemplace al ser humano falible todavía le queda un largo camino por recorrer.
Por ahora, los robots utilizados en las cadenas de producción de la mayoría de las fábricas de coches —para ensamblar y soldar— son muy primitivos.
Habitan un mundo "perfecto", y no tienen ninguna capacidad de sentir y reaccionar a su entorno.
Un importante campo de la investigación de la inteligencia artificial —la visión tridimensional— es crucial para la creación de sistemas prácticos.
Se desarrolla una amplia gama de técnicas para la selección de las características más sobresalientes de una imagen; esto permitiría, por ejemplo, que un robot reconociera y recogiera un objeto desde la línea de producción, incluso si el objeto no estuviera en su posición correcta.
¿Máquinas pensantes?:
El camino hacia la máquina pensante resulta ser más largo y más difícil de lo que pensaron los pioneros de la inteligencia artificial de la década de los 40 y 50.
Todavía existe un fuerte debate entre la comunidad de investigadores de la inteligencia artificial sobre si los ordenadores serán capaces algún día de pensar o de demostrar las características normalmente consideradas esenciales para la inteligencia.
Sin embargo, la búsqueda de la máquina pensante nos ha proporcionado robots, traducción automática, sistemas de ordenador capaces de obedecer órdenes verbales y de reconocer rostros, y un programa para jugar al ajedrez capaz de ganar a algunos de los maestros más destacados del mundo.
Mientras continúa el debate, la investigación de la inteligencia artificial nos proporciona una mejor comprensión del funcionamiento del cerebro y de nuestra propia inteligencia, y una profundización en temas como las disfunciones del habla y los problemas de aprendizaje.

Brazos de un robot trabajan en la cadena de ensamblaje de una planta de producción de coches.
------------- 00000 ------------
EL PRINCIPIO DE INCOMPATIBILIDAD:
Un paso fundamental en la aproximación entre el modo de razonamiento humano y el de la máquina es comprender que, en situaciones con determinado grado de complejidad, no existe una solución única, sino que pueden aplicarse métodos diversos.
La mente del ser humano es capaz de ponderar las ventajas e inconvenientes que ofrece cada uno y, en consecuencia, tomar una decisión. Normalmente, el ordenador se encuentro determinado hacia un único camino.
El principio de incompatibilidad de los sistemas complejos fue formulado en 1972 por Zadeh.
Expresa el hecho de que a medida que se profundiza en el estudio de las propiedades características de un determinado sistema, mayor riesgo de imprecisión y error existe para su descripción.
Al aumentar la complejidad, las posibilidades de expresarnos con exactitud y pertinencia disminuyen, en razón del número creciente de situaciones en estudio y de factores que intervienen en nuestro análisis.
Fuente Consultada: Enciclopedia Universal - Espasa-Calpe - Tomo 23
Temas Relacionados con el Razonamiento:
La Inteligencia Humana: Su medición (CI) y los Tipo de Inteligencia
Frases y Citas Sobre la Inteligencia:Célebres Pensamientos
Binet Alfredo Resumen de su Biografía y Obra Cientifica Escala y Test
Niños Superdotados o Prodigios:Comportamiento y Problemas
Acertijos de Sam Loyd Problemas Para Pensar
Ejercicios Elementales de Ciencia Para Razonar y Practicar
Enlace Externo:• 6 conceptos de Inteligencia Artificial






