Leyes de la Mecanica Clasica: Principios de Inercia y Masa -Ley Newton
Leyes de la Mecánica Clásica Las Leyes de Newton
Las Tres Leyes:
1-Principio de Inercia
2-Principio de Masa
3-Acción y Reacción
1) PRIMER PRINCIPIO: LA INERCIA
Los cuerpos quietos permanecen quietos a menos que se les aplique alguna fuerza para que comiencen a moverse.
Los cuerpos en movimiento permanecen en movimiento a menos que se les aplique alguna fuerza para detenerlos.
El principio de inercia es tan simple como decir que para cambiar la velocidad de un cuerpo es necesario aplicarle una fuerza, hacerle algo, interactuar con él.
De este modo, si un cuerpo se está moviendo con cierta rapidez en determinada dirección, seguirá en esa dirección y con la misma rapidez a menos que lo perturbemos.
Los cuerpos no cambian su velocidad (dirección y rapidez) si no reciben alguna fuerza.
En la física aristotélica entre los movimientos naturales se encontraba el de caída libre de una piedra.
La caída se debía a que la piedra tenía su lugar natural en el centro del universo que, según los aristotélicos, coincidía con el centro de la Tierra.
No hacía falta que una fuerza se ejerciera sobre la piedra, porque ella misma iría hacia su lugar natural.
Newton logró explicar la caída de la piedra de un modo totalmente diferente gracias a su descubrimiento de la ley de atracción gravitatoria.
La piedra cae porque es atraída gravitatoriamente por la Tierra. Si esta atracción no existiera, la piedra quedaría suspendida en el lugar en donde la abandonáramos.
 Por este mismo principio de inercia Newton describe el movimiento de una carreta en términos que difieren de los aristotélicos.
Por este mismo principio de inercia Newton describe el movimiento de una carreta en términos que difieren de los aristotélicos.
Antiguamente se creía que si los bueyes que tiran de una carreta se sueltan de ella, la carreta dejará de moverse porque ha cesado la fuerza que hacían los bueyes y “naturalmente” la carreta se detendrá, ya que el estado “natural” de la carreta es el reposo y no el movimiento.
Pero Newton sostiene que la carreta que está en movimiento no se detendrá a menos que se le aplique una fuerza, tal como lo describe el principio de inercia.
Entonces la carreta se detiene por la acción de una fuerza, ya que lo “natural” en la mecánica de Newton es la conservación del estado de movimiento.
Deberá haber alguna causa para la detención de la carreta.
Estas mismas diferencias se notan en cuanto al movimiento de los planetas.
Para Aristóteles, el movimiento circular alrededor del centro del universo no necesita una causa, es un movimiento natural.
Para Newton, además de que no cree que haya un centro del universo, el movimiento de los planetas alrededor del Sol necesita una fuerza que mantenga al planeta ligado al Sol, ya que si ninguna fuerza actuara sobre el planeta, éste se movería sin cambiar su velocidad tanto en rapidez como en dirección.
Es decir que si no existiera tal fuerza, el planeta se movería con rapidez constante en una línea recta. Newton propuso que esa fuerza era la atracción gravitatoria entre el Sol y el planeta.
Vemos que la idea de que los movimientos requieren alguna causa es muy antigua y se opone al pensamiento newtoniano de que los cambios en la velocidad son los que deben tener alguna causa.
En la visión newtoniana un movimiento de rapidez constante y en línea recta (conocido como movimiento rectilíneo uniforme) no necesita una causa. Una modificación de este estado de movimiento, sí la necesita.

► La Inercia en la Vida Diaria:
Por mas que no pensemos diariamente sobre la inercia, esta como la atracción gravitatoria y otras tantas características que estudiamos en física, te acompañan adonde tú vayas.
Por ejemplo, no puedes arrancar tan rápidamente como quisieras al comenzar a correr; tampoco puedes detenerte de golpe.
Tu cuerpo tiene inercia!.
Es necesario aplicarle una fuerza para que comience a moverse desde un estado de reposo.
También tienes que aplicar una fuerza para detenerte, ya que si no, tu cuerpo seguiría con la misma rapidez y en la misma dirección.
Si vienes corriendo alrededor de la manzana te costará bastante dar la vuelta a la esquina a gran velocidad puesto que la inercia de tu cuerpo hace que tengas que hacer un esfuerzo importante para cambiar la dirección de tu movimiento.
Cuando estás en un colectivo y arranca, si no te agarras fuertemente de algún pasamanos verás que tu cuerpo se queda en reposo mientras el colectivo gana velocidad.
Esto es muy divertido, siempre que no termines sentado arriba del pasajero del asiento del fondo,
Cuando el colectivo frena, algo similar te ocurre.

Tu cuerpo sigue andando hacia adelante y deberás agarrarte fuertemente para no terminar en la cabeza del chofer ni asomándote por el parabrisas (cosa nada recomendable aunque seas cabeza dura).
Los cinturones de seguridad nos protegen en caso de un impacto frontal. Los cinturones de seguridad comunes te los ajustas a tu medida y luego el largo queda fijo.
En cambio los cinturones de seguridad ; inerciales se diseñaron para que puedas moverte sin que el cinturón te tironee mientras que tus movimientos son suaves.
Solamente se traban en caso de que tu cuerpo siga andando hacia adelante por inercia cuando el automóvil se detuvo bruscamente.
Si el automóvil no se detiene bruscamente o tú te has atajado con las manos para no seguir andando por inercia, el cinturón no accionará su traba.
Para probar si el cinturón inercial está en buen funcionamiento, tira fuertemente de él como lo haría tu cuerpo durante la frenada o choque al seguir andando por inercia a la velocidad que traía el auto anteriormente.
Si el cinturón inercial se traba con un tiròn rápido, funciona correctamente; si no se traba, debe cambiarlo, ya que en esas condiciones no es un cinturón seguridad inercial sino una banda de adorno.
Los lavarropas con centrifugado han mejorado notablemente la calidad de vida.
Especialmente no necesitamos que el sea muy soleado para que la ropa se seque, ya que la centrifuga dejándola casi seca (según las propagandas). La centrifugación la forma en que usamos la inercia de las gotas de agua para secar la ropa. El tambor (batea) del lavarropas hacer dar vuelta la ropa a gran velocidad.
Si no fuera por la fuerza que la batea hace sobre la ropa, ésta seguiría andando en línea recta según el principio de inercia.
Pues bien, a alguien se le ocurrió hacer agujeritos en la batea para permitir que las gotas de agua frente agujerito pudieran seguir de largo. De este modo usamos la inercia de las gotas para desprenderlas de la ropa (o bien desprender la ropa del agua).
El juego del tejo sobre una mesa es apasionante y muestra algo de nuestro interés en este momento.
La mesa tiene agujeritos por donde sale aire , de modo que el tejo que suspendido sobre la mesa y así se evita el rozamiento entre la superficie de la mesa y el tejo.
Verás que si golpeas suavemente al tejo, se deslizará sobre la mesa a velocidad constante hasta que choque contra una de las paredes, o que tu contrincante le imprima un golpe o termine entrando por el arco marcando gol (preferiblemente en el arco contrario).
El principio inercia te sirve para explicar por qué el tejo se mueve con velocidad constante cuando nadie está tirando de él o empujándolo.
Por definición se dice: "Que la inercia es la tendencia a mantener el estado de movimiento reposo que posee un cuerpo"
► LA INERCIA:
La primera ley de Newton dice que “un objeto en reposo tiende a seguir en reposo y todo cuerpo en movimiento tiende a permanecer en movimiento con la misma velocidad, dirección y sentido a menos que el cuerpo interactúe con otros cuerpos”.
Es decir que los objetos “tienden a seguir haciendo lo que estaban haciendo”.
Hay una resistencia natural de los cuerpos que se oponen a cambiar su estado de movimiento.
Esta resistencia al cambio de estado de movimiento se llama inercia.
inercia = resistencia de un objeto a cambiar su estado de movimiento
Esta idea de Newton fue muy novedosa en su época, ya que se oponía a las concepciones que estaban de moda.
Como decíamos mas arriba, antes de Newton se pensaba que todos los cuerpos tenían una tendencia natural al estado de reposo.
Se creía que los objetos que se movían iban a detener su movimiento y que era necesario “hacerles algo” para mantenerlos en movimiento, pero que si se los dejaba libres de cualquier tipo de interacción, llegaban al reposo.
Se creía, entonces, que había una tendencia natural de los cuerpos a alcanzar su estado de reposo.
Galileo Galilei (antes que Newton) desarrolló el concepto de inercia.

Razonó que los cuerpos detenían su movimiento por una interacción de los cuerpos con su entorno, lo cual llamó fricción.
Para establecer y demostrar sus razonamientos, realizó experiencias usando dos planos inclinados enfrentados y dejando caer una pelota desde uno de ellos.
Galileo observó que sí una pelota rodaba hacia abajo desde una determinada altura, alcanzaba en el otro plano una altura similar a la inicial, y que cuanto más pulidos eran los planos, más cercana era la altura alcanzada con respecto a la inicial.
Galileo dedujo que la diferencia de altura observada se debía a la interacción de fricción de los cuerpos con la superficie del plano y que si esta no existiera, alcanzarían la misma altura.
Más adelante, concluyó que, independientemente de las orientaciones de los planos, los objetos alcanzaban la misma altura.
Resumiendo: si no hay fricción alcanza la misma altura y el ángulo se reduce, recorrerá más distancia hasta alcanzar la misma altura
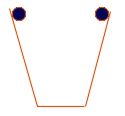

¿Qué sucede si el segundo plano no está inclinado?
Galileo concluyó diciendo que si el segundo plano no está inclinado, la pelota seguirá rodando sin cesar, buscando alcanzar la misma altura. si no hay fricción

aquí la pelota no se detiene nunca, sigue rodando y rodando...
Newton construyo sus ideas con los pensamientos de Galileo acerca del movimiento.
La primera ley de Newton establece que no es necesaria ninguna interacción para mantener un cuerpo en movimiento. Si deslizamos un libro sobre la mesa, vemos que después de un tiempo este se detiene, pero se detiene porque existe una interacción (que es la de la fricción entre el libro y la mesa) que se opone al movimiento, y no es la ausencia de la interacción lo que lo lleva al reposo.
Todos los objetos resisten al cambio del estado de movimiento.
Todos los objetos tienen esa tendencia, todos tienen inercia.
Pero aquí cabe una pregunta:
¿Tienen todos los objetos la misma tendencia a resistir el cambio?.
La respuesta es, obviamente, ¡No! Todos tienen inercia, pero la inercia de un cuerpo depende de la masa, es decir, de la cantidad de materia que posee un cuerpo.
A mayor cantidad de masa, mayor inercia y mayor resistencia al cambio del estado de movimiento.
2) SEGUNDO PRINCIPIO: DE MASA
Recién vimos que para que un cuerpo quieto comience a moverse es necesario aplicar una fuerza sobre él.
Además nos damos cuenta de que cuanto mayor es la fuerza que aplicamos tanto más se acelera.
También sabemos que para acelerar a algunos cuerpos es necesario aplicarles más fuerza que a otros para lograr el mismo efecto.
Para lograr la misma aceleración a unos cuerpos hay que aplicarles más fuerza y a otros menos.
Esto se debe a que algunos cuerpos tienen más inercia y otros menos inercia. No es lo mismo acelerar un tren que una bicicleta.
La inercia del cuerpo es una de sus propiedades y, para determinarla, podríamos preguntarnos cuánta fuerza es necesario aplicarle al cuerpo para obtener una determinada aceleración.
Entonces la cantidad de fuerza para obtener cierta aceleración es una medida de la inercia. Si un cuerpo tiene mucha inercia, entonces hace falta mucha fuerza para acelerarlo con cierto valor.
Si un cuerpo tiene poca inercia, entonces hace falta poca fuerza para acelerarlo con ese mismo valor.
Un problema adicional que tenemos cuando queremos medir la inercia de un cuerpo es que puede haber varias fuerzas actuando sobre el cuerpo y darnos una falsa impresión de lo difícil que resulta acelerarlo.
Por ejemplo, el automóvil de Pedro se ha quedado sin nafta y su hermano y yo queremos darle una mano para que llegue a la estación de servicio de la esquina.
Mientras los tres empujamos, el hermano de Pedro piensa: “Este automóvil tiene poca inercia porque yo hago poca fuerza y se acelera bastante”.
Al llegar a la estación Pedro y yo tratamos de detenerlo, pero el hermano de Pedro sigue haciendo fuerza para empujarlo sin que nos demos cuenta de ello.
A nosotros nos parecerá que el automóvil tiene mucha inercia porque es difícil detenerlo.
La manera de resolver el problema es hacer la cuenta del total de fuerzas que están actuando; determinar cuál es el valor de la fuerza neta aplicada (a la que se suele llamar “resultante’).
Para eso recordemos que las fuerzas son vectores y que debemos sumarias y restarlas vectorialmente.
En el ejemplo del auto de Pedro es muy sencillo, ya que las fuerzas están aplicadas en la misma dirección (longitudinalmente al automóvil), aunque algunas con sentido hacia adelante y otras con sentido hacia atrás.
La medida de la inercia se podrá obtener comparando la fuerza neta aplicada, o resultante y la aceleración obtenida.
• Equilibrio, reposo y movimiento
Cuando vemos el libro de física sobre la mesa entendemos que para empezar a moverlo hace falta una fuerza que lo acelere.
También sabemos que el libro tiene la fuerza de su peso aplicada sobre él (en dirección vertical y hacia abajo).
Entonces sobre el libro ya están actuando fuerzas. ¿Por qué entonces no se acelera en la dirección de esa fuerza?.
La respuesta la encontramos fácilmente si tenemos en cuenta que lo que modifica la velocidad de un cuerpo es la fuerza neta o fuerza total aplicada, tal como lo vimos en la sección anterior.
Como el libro sigue en reposo, la fuerza total debe ser nula. Debe haber otra fuerza que lo está sosteniendo.
Una fuerza que se opone al peso y que es de la misma intensidad, de modo que la suma sea cero.
Pregunta: ¿Qué cuerpo ejerce una fuerza sobre el libro de modo de impedir su caída?
Si saco la mesa, el libro se acelerará en caída libre hacia el piso.
De este modo vemos que existen dos fuerzas que actúan sobre el libro: la fuerza peso ejercida por la Tierra sobre el libro (por la atracción gravitatoria mutua) y la fuerza que impide la caída del libro,
Decimos que el libro está en equilibrio cuando permanece en reposo durante un lapso. Vemos que cuando esto ocurre la suma de fuerzas aplicadas sobre él es cero.
Podríamos reinterpretar el principio de inercia diciendo que todo cuerpo que está en equilibrio no se acelera.
Pero, ¿qué pasa con los cuerpos que están en movimiento? ¿Están en equilibrio o no?.
Es fácil responder a estas preguntas si pensamos en el principio de inercia.
Por ejemplo, aunque el avión vaya a gran velocidad, si la azafata nos convida con una gaseosa, el vaso, la gaseosa y nosotros estamos en equilibrio; ya que la suma de las fuerzas es cero y no nos estamos acelerando.
Si en cambio la suma de las fuerzas no es cero (el avión está despegando o hay “pozos de aire”), sí hay aceleración.
Resumiendo, el que veamos algo en movimiento no indica que la fuerza total o resultante sea distinta de cero.
Todos los movimientos en los que no cambia la velocidad son casos en donde la suma de fuerzas es cero.
No hace falta que haya una fuerza neta aplicada para que algo se esté moviendo (con velocidad constante).
En cambio, sí hace falta alguna fuerza neta aplicada para que empiece a moverse, para que deje de moverse o para que cambie su velocidad en dirección o rapidez.
Cuando decimos que algo está en equilibrio indicamos que la suma de fuerzas es cero, pero no damos información de si el cuerpo está en reposo o en movimiento con velocidad constante.
No se de que se trata, pero me opongo al rozamiento:
Cuando por ejemplo, queremos empujar un sillón notamos que hay que hacer cierto esfuerzo para que se ponga en movimiento.
Esto es razonable si recordamos el principio de inercia.
Según este principio, una vez en movimiento el sillón seguiría andando aunque no lo empujáramos (como en el caso de la carreta a la que se le soltaron los bueyes).
Sin embargo, observamos que si no seguimos aplicando una fuerza el sillón se detiene.
Entonces, cuando el sillón está en movimiento alguna fuerza está actuando en contra de su movimiento.
Esa fuerza es la de rozamiento entre el sillón y el piso.
Por eso tenemos que mantener cierta fuerza aplicada para lograr que el sillón siga andando con velocidad constante.
La fuerza que debemos aplicar es la misma cantidad que la fuerza de rozamiento y de esa manera la fuerza total es cero y el sillón no se detendrá:
Fuerza para empujar el sillón-fuerza de rozamiento=0
Se puede así obtener un movimiento de velocidad constante aun cuando estemos aplicando fuerza sobre el sillón, ya que la que aplicamos nosotros más la de rozamiento se anulan y el sillón no se acelera.
Si queremos acercar el sillón hacia la ventana, el rozamiento es una fuerza que parece estar en contra de ese movimiento.
Si queremos alejar el sillón de la ventana, también el rozamiento se opone.
No importa en qué dirección intentemos mover un cuerpo, las fuerzas de rozamiento tienen sentido contrario a ese movimiento.
Cuando el piso es de baldosas es más fácil desplazar el sillón; cuando el piso es de goma es muy difícil desplazarlo.
La fuerza de rozamiento depende de las superficies que están en contacto (el piso y el sillón) y de cuánto está comprimida una superficie contra otra,
Un análisis detallado de las fuerzas de rozamiento nos llevaría a estudiar las fuerzas entre las moléculas de las superficies en contacto, pero podemos entender las fuerzas de rozamiento como algo parecido a cuando una superficie está poco pulida y entonces es más difícil deslizarse sobre ella.
Además del rozamiento entre dos superficies en contacto existe el rozamiento de los fluidos.
Cuando queremos desplazarnos en medio del agua, sentimos que es mas costoso.
Distintos fluidos oponen distinta fuerzas de rozamiento.
El rozamiento con el agua es menor que con el dulce de leche. El aire también es un fluido y opone rozamiento a desplazarse a través de él.
Si movemos la mano lentamente en el agua, no parece haber mucha fuerza que se oponga al movimiento,
Pero si intentamos moverla rápidamente1 veremos que la fuerza es bastante notoria.
Con el aire y los demás fluidos pasa lo mismo.
El rozamiento de los fluidos crece con a rapidez y esto será interesante para analizar los saltos de paracaidismo.
► Por fin el principio de masa
Supongamos que a un carrito le aplicamos cierta fuerza neta y el carrito se mueve con determinada aceleración.
Veremos que si en una segunda prueba la fuerza que le aplicamos al carrito es el doble que en a primera prueba, entonces la aceleración con la que se moverá en este caso será el doble de la aceleración anterior.
Este experimento sencillo nos muestra que para cada cuerpo la fuerza aplicada y la aceleración obtenida son proporcionales.
O bien, que el cociente entre la fuerza y a aceleración es un valor constante y que sólo depende del cuerpo con el que estemos experimentando.
F/a = cte
Newton descubrió esta proporcionalidad entre la fuerza y la aceleración, y a la constante de proporcionalidad la llamó “masa” del cuerpo.
Así, pues, la masa del cuerpo mide la cantidad de inercia que tiene ese cuerpo.
El segundo principio de Newton dice que la fuerza que se le aplica a un cuerpo y la aceleración que éste adquiere debido a esa fuerza son magnitudes proporcionales y que la constante de proporcionalidad es la masa del cuerpo.
Lo podríamos entender de otro modo diciendo que la fuerza total aplicada sobre un cuerpo produce una aceleración y que los valores de la fuerza aplicada, a aceleración y la masa del cuerpo cumplen con la ecuación: F=m.a
Recordemos que tanto F como a son vectores y que el cuerpo se acelera en la dirección y sentido en que actúa la fuerza neta aplicada.
En cambio la masa es una magnitud escalar (no tiene dirección ni sentido) y puede medirse con un número en las unidades que se elijan para ello. En general se utiliza como unidad de masa el kilogramo o el gramo.
• Volumen, peso y masa
No cabe duda de que un elefante es más grande que un raes más pesado y tiene más inercia.
Sin embargo, estas tres magnitudes se pueden distinguir con un poco de atención.
Estamos acostumbrados a estimar el peso de las bolsas por el tamaño pero más de una vez nos llevamos una sorpresa.
Alguna bolsas de gran tamaño tienen menos peso que otras bolsas pequeñas.
Es fácil de entender por ejemplo si han cargado la bolsa más pequeña con tornillos y la más grande con plumas.
Así distinguimos fácilmente el volumen del peso.
El volumen asociado a las dimensiones, es el espacio que ocupa el cuerpoo.
El peso es la fuerza con la que el cuerpo es atraído por la Tierra.
También sabemos que los astronautas en la Luna dan grande saltos porque en la Luna pesan menos.
Más aún, en el espacio exterior los cuerpos no tienen peso porque no están cerca según planeta o luna como para que se note que los atrae gravitatoriamente.
Así, el peso es una fuerza que aparece sólo en las cercanías de la Tierra, la Luna o algún otro astro.
Lo que pesa una persona depende de la persona y de dónde se suba a la balanza, en la Tierra, la Luna, en el espacio...).
El valor del peso depende dos cuerpos: la persona y el planeta en donde se está pesando
La masa, en cambio, es la inercia que tiene un cuerpo.
Es su propiedad por la cual es necesaria cierta cantidad de fuerza para arlo. Y esto no desaparece en ninguna parte del espacio, pende de que esté cerca o lejos de algún planeta.
Es una propiedad del cuerpo.
Para que un astronauta acelere una lata de gaseosa en el espacio, necesitará aplicarle la misma fuerza que para acelerarla aquí en la Tierra.
Recuerda que la masa (la inercia) mpaña adonde tú vayas.
• Velocidad Terminal
Vimos que, cuando el rozamiento con el aire es muy pequeño, los cuerpos caen con una aceleración g (9,8 m/seg2).
Esta es a aceleración de la gravedad y se debe a la atracción gravitatoria de a Tierra sobre el cuerpo que cae.
Pero la fuerza de atracción gravitatoria aplicada sobre el cuerpo es su peso, y entonces podemos decir que el cuerpo se acelera debido a a fuerza de su peso.
Así, la expresión del principio de masa para el caso de un cuerpo en caída libre se transforma en:
P= m.g
El peso es un vector que apunta para abajo (hacia centro de la Tierra) y la aceleración g también.
En esta expresión del segundo principio se ve la relación entre peso, masa y aceleración de la gravedad.
Pero ¿qué pasa si el rozamiento con el aire no es despreciable? .
En ese caso no podremos asegurar que el cuerpo con la aceleración g ya que no sólo el peso es el que actuando sino también la fricción con el aire.
Como la friccion con el aire (FR) es una fuerza contraria (opuesta) al sentido del movimiento, el segundo principio toma la forma:
P-FR =m.a en donde la fuerza neta que actúa sobre el cuerpo en caída es la diferencia entre el peso y la fricción.
Como esta fuerza neta es un poco menor que el peso, la aceleración a será menor que g.
Habrás notado que al sacar una mano por la ventanilla de un auto se puede sentir la fuerza de fricción del aire.
También te habrás dado cuenta de que cuanto más rápido va el auto mayor es la fuerza de fricción.
Entonces, cuando un paracaidista salta desde un avión, a medida que va más rápido debido a su aceleración de caída, cada vez tiene mayor rozamiento con el aire.
Llegará un momento en que el rozamiento sea tan intenso como la fuerza peso del paracaidista, y en ese caso la fuerza neta sobre él será cero:
P=FR o bien: P-FR =0
La velocidad a la que esto ocurre es la velocidad límite o velocidad terminal.
A partir de allí, como la fuerza neta aplicada es cero (mientras que no se abra el paracaídas), el paracaidista no se acelera más.
Su aceleración es también cero (de la ecuación) y se mantiene una caída a velocidad constante (por lo cual se la llama “velocidad límite”).
Que masa tiene una pesa - Cuánto pesa una masa
Las pesas que se usaban en las balanzas antiguas funcionaban como medida de comparación para saber cuántas manzanas o bizcochos se compraban.
Un cuerpo que tenga una masa de un kilogramo debe pesar una cierta cantidad que se puede calcular según la fórmula: P=m.g
Reemplazando: 1kg. . 9.8 m/seg2 =9.8 Kg.m/seg2
Como es muy habitual medir la distancia en metros, la masa en kilogramos y el tiempo en segundos, a esta elección de unidades de medida se la llama “Sistema MKS’. En este sistema al producto: kg . m/seg2 se lo llama newton (N), por lo cual queda
P = 9,8 N
Así, un kilogramo de masa pesa 9,8 N.
También podemos preguntarnos qué masa tiene un cascote que pesa 1 N..
En ese caso haremos la cuenta despejando la masa: m = P/g
Obtenemos que el cascote tiene una masa de 102 gramos.
En el Sistema Técnico, en cambio, se utiliza una unidad de fuerza que facilita los cálculos entre masa y peso.
Esta unidad se llama «kilogramo fuerza”(kgf). Se propone esta unidad de modo que un kilogramo de masa pese un kilogramo fuerza.
Entonces, si el peso de un kilogramo de masa es 9,8 N y en el otro sistema es 1 kgf, tenemos la equivalencia: 9,8 N= 1 kgf
El kilogramo fuerza es muy útil porque para asegurarse de que se cuenta con una masa de 3 kilogramos basta con asegurarse de que pese 3 kgf y no hace falta hacer la cuenta de cuántos newtons pesan 3 kg.
Pero por otra parte produce cierta confusión, si no se recuerda bien que el kgf es una unidad de fuerza y un kg es una unidad de masa.

EJEMPLO DE LA 2º LEY DE NEWTON APLICADA A UN ASCENSOR
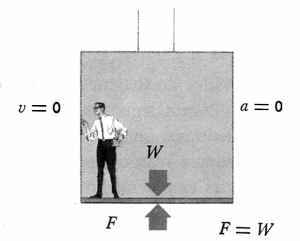
Si el elevador no se mueve, el piso empuja los pies con una fuerza (F) igual al peso del pasajero (W).
Estas fuerzas se equilibran y el pasajero está en equilibrio.
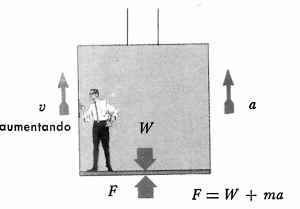
Mientras el elevador acelera hacia arriba , el piso empuja los pies del pasajero con una fuerza igual a su peso (W) más una fuerza aceleradora (ma); las fuerzas hacia abajo y hacía arriba están desequilibradas.
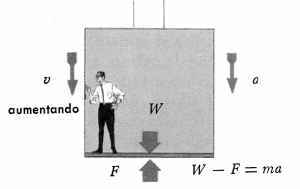
Cuando el elevador acelera hacia abajo el peso del pasajero es mayor que la fuerza dé sustentación del elevador. En consecuencia, el pasajero acelera hacia abajo. W — F es la fuerza no equilibrada, que causa la aceleración.
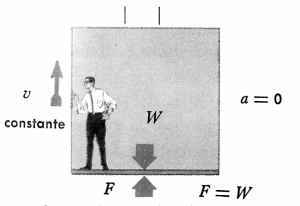
Cuando el elevador se mueve con velocidad constante, no se necesita fuerza para acelerar. Por tanto, el elevador empuja al pasajero con una fuerza igual a su peso. Las fuerzas están equilibradas y el pasajero está en equilibrio.
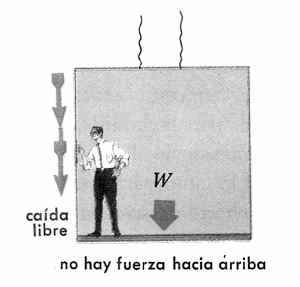
Si los cables que sostienen el elevador se rompen y éste desciende en caída libre, el elevador y pasajero caen con la misma rapidez. La fuerza hacia arriba en los píes es 0.
El peso, que actúa hacia abajo, hace caer al pasajero, pero como no hay presión en las suelas de sus zapatos, tiene la sensación de ingravidez o falta de peso. Esta es la sensación que un cosmonauta tiene, cuando está navegando en el espacio.

3)TERCER PRINCIPIO: ACCION Y REACCION
Cierto día estaba en mi automóvil detenido frente a la luz roja del semáforo esperando mi turno, cuando de pronto: CRASH!!
Un conductor distraído achicó mi baúl y me dejó sin luces traseras.
Ambos descendimos para contabilizar los daños y el distraído me mostraba cómo mi baúl le había abollado la trompa de su último modelo.
Yo me quejaba de que mi baúl había desaparecido como si fuera plegable, pero él insistía en que mi auto le había roto sus nuevos faros de gran alcance, ¿qué otra cosa podía haber actuado sobre su auto?.
Seguro que mi auto era el causante de su abolladura.
Por otra parte su auto era el que había hecho fuerza sobre mi baúl para plegarlo de esa manera. Los dos automóviles habían interactuado.
El auto del distraído hizo fuerza sobre el mío y el mío hizo fuerza sobre el suyo.
Nunca había pensado que el principio de interacción se encargaría de los accidentes de tránsito.
Cada vez que un cuerpo ejerce una acción sobre otro empujándolo tirando de él, atrayéndolo gravitatoriamente o magnéticamente, chocándolo o acariciándolo, se produce una interacción éntre ambos.
Un cuerpo aplica una fuerza sobre otro y a su vez recibe del otro una fuerza de igual intensidad pero de sentido contrario.
Por cada par de cuerpos que están interactuando aparece un par de fuerzas.
La Tierra atrae gravitatoriamente a la Luna y es atraída por la Luna con una fuerza de igual intensidad.
El martillo ejerce una fuerza sobre el clavo y así logramos que el clavo se hunda en la madera, pero a su vez el clavo ejerce sobre el martillo una fuerza igual en intensidad pero de sentido contrario.
Esta fuerza sobre el martillo es la que detiene el martillo e incluso lo hace «rebotar» hacia arriba.
Cuando nuestro automóvil lleva un remolque (de casa rodante o de lancha o moto), el remolque recibe una fuerza de nuestro auto.
Esta es la fuerza hacia adelante que acelera al remolque. Pero sobre nuestro auto actúa una fuerza hacia atrás de igual intensidad.
Esta fuerza hacia atrás sobre nuestro auto nos obliga a gastar más nafta que si no tuviéramos remolque para lograr la misma aceleración.
Las fuerzas del par de interacción son vectores como todas las fuerzas, pero tienen ciertas características:
1) Son de la misma intensidad.
2) Tienen sentidos opuestos.
3) Están en la misma recta de acción (tienen la misma dirección).
4) Una de ellas está aplicada en uno de los dos cuerpos que interactúan, y la otra, en el otro cuerpo.
A las dos fuerzas del par se las suele llamar “acción» y “reacción".
Alguien podría pensar que el auto tira del remolque con una acción y que entonces el remolque reacciona tirando del auto en sentido contrario.
Pero nosotros simplemente hablaremos de pares de interacción sin hacer esta diferencia.
Por ejemplo, la Tierra y la Luna se atraen gravitatoriamente.
Esta atracción es mutua.
No parece útil decir que la atracción que la Luna ejerce sobre la Tierra es la reacción y que la atracción que la Tierra ejerce sobre la Luna es la acción.
Podríamos clasificarlas al revés y también sonaría raro.
Preferiremos hablar de pares de fuerzas que aparecen en la interacción.
Definición: " A toda acción hay una reacción de igual magnitud, pero de sentido contrario"
Temas Relacionados:
Pasos del Metodo Cientifico Etapas Metodo Experimental
El desarrollo cientifico y grandes inventos en el siglo XX
Los cientificos del siglo XIX:Descubrimientos y Avances
El Conocimiento Científico La Fisica y de la Naturaleza
Biografia de Max Planck: Científico Creador de la Teoría Cuántica
Historia de Ciencia Tecnica Tecnologia y Sus Avances
Biografia de Cavendish Su Trabajo Cientifico






