Teorema Fundamental de la Hidrostática:Demostración del Principio
Teorema de la Hidrostática
Demostración del Principio de Arquímedes
►El teorema fundamental de la hidrostática
¿Por qué las paredes de un dique van aumentando su espesor hacia el fondo del lago? ¿Por qué aparecen las várices en las piernas?
Es un hecho experimental conocido que la presión en el seno de un líquido aumenta con la profundidad.
Busquemos una expresión matemática que nos permita calcularla.
Para ello, consideremos una superficie imaginaria horizontal S, ubicada a una profundidad h como se muestra en la figura de la derecha.
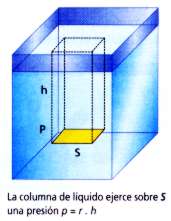 La presión que ejerce la columna de líquido sobre la superficie amarilla será:
La presión que ejerce la columna de líquido sobre la superficie amarilla será:
p = Peso del líquido/Area de la base
Con matemática se escribe: p = P/S = (d . V)/S=(d . S . h)/S= d . h (porque la S se simplifican)
donde p es el peso específico del líquido y V es el volumen de la columna de fluido que descansa sobre la superficie S.
Es decir que la presión que ejerce un líquido en reposo depende del peso específico (p) del líquido y de la distancia (h) a la superficie libre de éste.
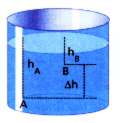 Si ahora consideramos dos puntos A y B a diferentes profundidades de una columna de líquido en equilibrio, el mismo razonamiento nos permite afirmar que la diferencia de presión será:
Si ahora consideramos dos puntos A y B a diferentes profundidades de una columna de líquido en equilibrio, el mismo razonamiento nos permite afirmar que la diferencia de presión será:
PA —PB = p . hA— d . hB
Este resultado constituye el llamado teorema fundamental de la hidrostática:
La diferencia de presión entre dos puntos dentro de una misma masa líquida es el producto del peso específico del líquido por la distancia vertical que los separa.
Ésta es la razón por la cual dos puntos de un fluido a igual profundidad estarán a igual presión.
Por el contrario, si la presión en ambos puntos no fuera la misma, existiría una fuerza horizontal desequilibrada y el líquido fluiría hasta hacer que la presión se igualara, alcanzando una situación de equilibrio.
Hasta aquí sólo hemos encontrado la expresión de la presión que ejerce el líquido sobre un cuerpo —imaginario o no— sumergido en una determinada profundidad h.
Ahora bien, ¿cuál es la presión total ejercida en el cuerpo?.
Si tenemos en cuenta que, probablemente, por encima del líquido hay aire (que también es un fluido), podemos afirmar que la presión total ejercida sobre el cuerpo es debida a la presión de la columna del líquido más la presión que ejerce el aire sobre la columna. Es decir:
P = Paire + Plíquido = Patmosférica + d . h
Este resultado tiene generalidad y puede ser deducido del teorema fundamental de la hidrostática. Veamos cómo. Si consideramos que el punto B se encuentra exactamente en la superficie del líquido, la presión en A es:
PA= PB+ d . Ah = Psuperficie + P. (hA-hB) = Patmosférica + d . h
Los vasos comunicantes son recipientes comunicados entre sí, generalmente por su base. No importa cuál sea la forma y el tamaño de los recipientes; en todos ellos, el líquido alcanza la misma altura.
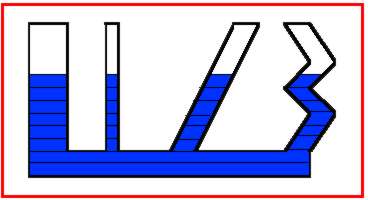
Cuando tenemos un recipiente vertical conteniendo un liquido y le hacemos perforaciones en sus paredes, las emisiones del liquido de los agujeros de la base tendrán mayor alcance que las emisiones de arriba, ya que a mayor profundidad hay mayor presión.
► EL EMPUJE: PRINCIPIO DE ARQUIMEDES
Resulta evidente que cada vez que un cuerpo se sumerge en un líquido es empujado de alguna manera por el fluido.
A veces esa fuerza es capaz de sacarlo a flote y otras sólo logra provocar una aparente pérdida de peso.
Pero, ¿cuál es el origen de esa fuerza de empuje? ¿De qué depende su intensidad?
Sabemos que la presión hidrostática aumenta con la profundidad y conocemos también que se manifiesta mediante fuerzas perpendiculares a las superficies sólidas que contacta.
Esas fuerzas no sólo se ejercen sobre las paredes del contenedor del líquido sino también sobre las paredes de cualquier cuerpo sumergido en él.
• Distribución de las fuerzas sobre un cuerpo sumergido
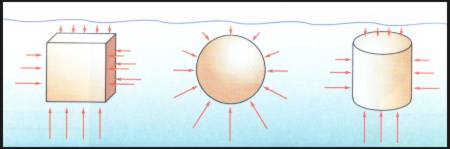
Imaginemos diferentes cuerpos sumergidos en agua y representemos la distribución de fuerzas sobre sus superficies teniendo en cuenta el teorema general de la hidrostática.
La simetría de la distribución de las fuerzas permite deducir que la resultante de todas ellas en la dirección horizontal será cero.
Pero en la dirección vertical las fuerzas no se compensan: sobre la parte superior de los cuerpos actúa una fuerza neta hacia abajo, mientras que sobre la parte inferior, una fuerza neta hacia arriba.
Como la presión crece con la profundidad, resulta más intensa la fuerza sobre la superficie inferior. Concluimos entonces que: sobre el cuerpo actúa una resultante vertical hacia arriba que llamamos empuje.
• ¿Cuál es el valor de dicho empuje?
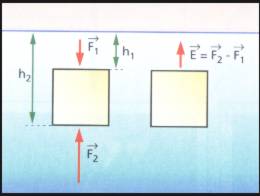
Tomemos el caso del cubo: la fuerza es el peso de la columna de agua ubicada por arriba de la cara superior (de altura h1).
Análogamente, F2 corresponde al peso de la columna que va hasta la cara inferior del cubo (h2).
El empuje resulta ser la diferencia de peso entre estas dos columnas, es decir el peso de una columna de líquido idéntica en volumen al cubo sumergido.
Concluimos entonces que el módulo del empuje es igual al peso del líquido desplazado por el cuerpo sumergido.
Con un ejercicio de abstracción podremos generalizar este concepto para un cuerpo cualquiera.
Concentremos nuestra atención en una porción de agua en reposo dentro de una pileta llena.
¿Por qué nuestra porción de agua no cae al fondo de la pileta bajo la acción de su propio peso?.
Evidentemente su entorno la está sosteniendo ejerciéndole una fuerza equilibrante hacia arriba igual a su propio peso (el empuje).
Ahora imaginemos que “sacamos” nuestra porción de agua para hacerle lugar a un cuerpo sólido que ocupa exactamente el mismo volumen.
El entorno no se ha modificado en absoluto, por lo tanto, ejercerá sobre el cuerpo intruso la misma fuerza que recibía la porción de agua desalojada. Es decir:
Un cuerpo sumergido recibe un empuje vertical y hacia arriba igual al peso del volumen de líquido desplazado.
E = Peso del líquido desplazado = dlíq . g . Vliq desplazado = dliq . g . Vcuerpo
Es importante señalar que es el volumen del cuerpo, y no su peso, lo que determina el empuje cuando está totalmente sumergido.
Un cuerpo grande sumergido recibirá un gran empuje; un cuerpo pequeño, un empuje pequeño.

Como hace un barco para flotar?
Pues bien, el mismo está diseñado de tal manera para que la parte sumergida desplace un volumen de agua igual al peso del barco, a la vez, el barco es hueco (no macizo), por lo que se logra una densidad media pequeña.
En el caso de los submarinos, tienen un sistema que le permite incorporar agua y de esta manera consiguen regular a sus necesidades la densidad media de la nave.
Él agua, el alcohol y el mercurio son líquidos, pero el principio de Arquímedes se aplica a todos los fluidos, es decir, también a los gases. Los gases fluidos son mucho menos densos y producen empujes mucho menores. Con todo, los objetos pesan menos en el aire de lo que pesarían en el vacío.
Un globo lleno de hidrógeno puede flotar en el aire porque su peso —que tiende a arrastrarlo hacia la Tierra— está exactamente equilibrado por el empuje del aire. Este empuje es también igual al peso de aire desplazado.
El conocimiento del principio de Arquímedes es de gran importancia para todo aquél que se ocupe del proyecto de barcos y submarinos, cuyo empuje debe ser calculado.
Es absolutamente esencial saber cuánto se hundirá un barco al ser botado, o cuál será el empuje de un submarino.
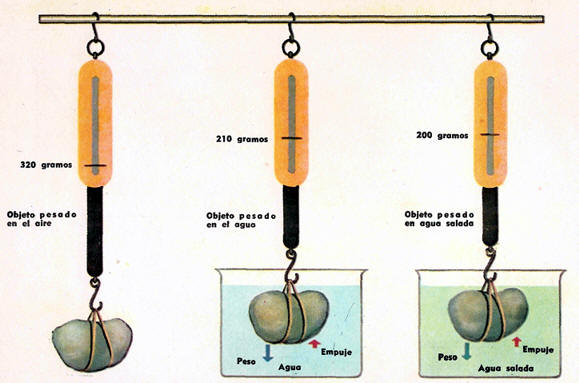
LA FLOTABILIDAD Y EL PRINCIPIO DE Arquímedes.
El objeto pesa menos en agua que en aire. La pérdida aparente de peso se debe al empuje del agua sobre el objeto. Pesa aún menos en agua salada.
Como el agua salada es más pesada que el agua dulce, el peso del líquido desplazado es mayor.
El empuje sobre el objeto es mayor porque es igual al peso de agua salada desalojada. Debido a este mayor empuje es más fácil flotar en agua salada que en agua dulce. Cuanto más denso el líquido, tanto más fácil será flotar en él.
EL PROBLEMA DE LA CORONA DEL REY
El rey Hierón le entregó 2,5 kg de oro a su joyero para la construcción de la corona real.
Si bien ése fue el peso de la corona terminada, el rey sospechó que el artesano lo había estafado sustituyendo oro por plata en el oculto interior de la corona.
Le encomendó entonces a Arquímedes que dilucidara la cuestión sin dañar la corona.
Con sólo tres experiencias el sabio pudo determinar que al monarca le habían robado casi un kilo de oro. Veamos cómo lo hizo.
En primer lugar, Arquímedes sumergió una barra de medio kilo de oro puro y comprobó que desplazaba 25,9 cm3. Por lo tanto, el peso específico del oro es:
Poro = 500 gr/25.3 cm3 =19.3 gr/cm3
Si el joyero hubiera hecho las cosas como le habían indicado, el volumen de líquido desplazado por la corona real, que pesaba 2,5 kilogramos, debería haber sido:
Vcorona = 2.500 gr/19.3 gr/cm3=129.5 cm3
A continuación, sumergió la corona real y midió que el volumen de agua desplazado era de 166 cm3, o sea, mayor del esperado.
¡Hierón había sido estafado!. ¿En cuánto?.
Para saber qué cantidad de oro había sido reemplazado por plata, Arquímedes repitió la primera experiencia sumergiendo una barra de un kilo de plata para conocer su peso específico.
Como el volumen desplazado resultó 95,2 cm3, se tiene que:
Pplata=1000 gr/95.2 gr/cm3=10.5 gr/cm3
Sabemos que el peso total de la corona es 2.500 gr. (el joyero tuvo la precaución de que así fuera) y su volumen total, de 166 cm3. Entonces:
Vcorona=Voro+Vplata=166 cm3
Vplata=166-Voro
Pcorona=Poro+Pplata=2500 gr.
Si reescribimos la última ecuación en función del peso específico y el volumen, nos queda que:
19.3 gr/cm3 . Voro + 10.5 gr/cm3 . Vplata = 2500 gr
Tenemos dos ecuaciones con dos incógnitas (Voro y Vplata). Sustituyendo una ecuación con la otra, se tiene que:
19,3 gr/cm3. Voro + 10.5 gr/cm3. (166 cm3-Voro) = 2.500 g
de donde se despeja la incógnita:
Voro =86cm3
con lo que se deduce que:
Poro =Poro Voro = 19,3 gr/cm3 . 86 cm3 = 1.660 gr
Pplata=Pcorona - Poro =2.500gr -1.660 gr =840 gr
De esta manera, Arquímedes pudo comprobar que al rey le habían cambiado 840 gr. de oro por plata.
Cuenta la leyenda que el joyero no pudo disfrutar del oro mal habido.
Temas Relacionados:
Teorema Fundamental de la Hidrostática
Teorema del Principio de Pascal
Concepto de Momento Flector o Cupla,Generos de Palancas
Maquinas Simples: Tipos de Palancas, Poleas, Plano Inclinado
Principio de Funcionamiento de Maquina Termicas
Ejercicios Elementales de Ciencia, Con Problemas Para Razonar
Uso de las Fuerzas Naturales:Aplicaciones del Viento, Calor y Agua
Tres Principios Basicos de la Física:Pascal Arquimides y Bernoullie
Leyes de la Mecanica Clasica: Principios de Inercia y Masa -Ley
Enlace Externo:•






