Resolución Geométrica de una Ecuacion de Segundo Grado:Metodo Arabe
Resolución Geométrica o Gráfica Ecuación de Segundo Grado-Metodo Arabe
ANTIGUO MÉTODO CREADO EN EL AÑO 800, POR UN UN MATEMÁTICO ÁRABE, CONOCIDO COMO MUSA AL-KHWARIZMI (780-850).
Quiero mostrarte una forma muy ingeniosa de resolver ecuaciones de segundo grado , en una etapa en donde la matemática estaba “en pañales”.
Este matemático trabajó en la biblioteca de Bagdad, cuando esta ciudad reemplazó a la gran Alejandría como centro cultural del mundo.
Poco se sabe de este hombre, pero si, se confirmó, que escribió unas pocas pero importantes obras sobre aritmética y álgebra, con numerosas aplicaciones practicas.
Estudió 6 casos de ecuaciones de segundo grado, y a la incógnita X la llamaba: “cosa”.
Como en aquella época no había un lenguaje estructurado para escribir ecuaciones, y menos, métodos algebraicos para resolverlas, este matemático (al igual que todos), recurrió a la geometría para resolver estas ecuaciones.
Cuando tienes una ecuación de primer grado (la incógnita X, no tiene exponente), la solución solo consiste en ir despejando los términos hasta dejar “solita la X”, y listo.
Por ejemplo: 3X+4=10 de donde X=(10-4)/3 , x=2
Nota que pasé primero el 4 restando al 10 porque estaba sumando, luego el 3 dividiendo porque estaba multiplicando y la X quedó sola en un miembro, y vale 2.
Bien, el problema aparece, cuando la X se eleva al número 2, entonces, queda: X², es decir elevada al cuadrado. Ahora como se hace para dejar sola a la X.
Actualmente (y desde hace siglos), hay un “formulita” muy simple para obtener el valor de X en estos casos, y en cualquier libro de matemática media la puedes encontrar, para no complicarla ahora.
Ejemplo de ecuación de segundo grado:
3x²-6x-10=0
Llevando este problema a 1200 años atrás, donde esas técnicas aun no existían, los matemáticos debieron agudizar su ingenio para tratar de resolver algunos casos de este tipo de ecuaciones, sobre todo porque tenían mucho uso en la vida práctica, donde se calculaban superficies, volúmenes, etc.
Te explicaré esta técnica, conocida como de “completar cuadrados”, utilizando el número de oro (muy usado en el libro Código de Da Vinci), que justamente viene determinado mediante una ecuación de segundo grado.
La proporción áurea es aquella, que respeta la siguiente condición, entre los segmento de la figura:
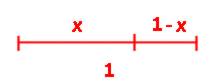
El cociente entre el segmento menor y el mayor debe ser igual al cociente entre el segmento mayor y el largo total del segmento, que en este caso vale 1.(puede ser 1 metro, 1 kilometro, 1 centímetro, etc).
En número ò en el lenguaje de las matemática es:
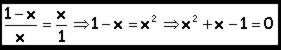
Observa la última ecuación y notarás que es de 2do. Grado. Resolver esto hoy, es “cosa de chicos” y si aplicas la fòrmula o resolvente de 2do. Grado como se la conoce, obtendrás el número de oro :X= 0.618......
Te mostraré como hizo este árabe para calcular el valor de X, sin despejar nada, ni usar formulas.
A la ecuación: x²+x-1=0
La pone asì: x²+x=1 (pasa el 1 restando al otro miembro como suma)
Supone lo siguiente:
El primer miembro: x²+x, dice (y tiene razón) que le representa la superficie lateral de una caja (como de zapatos), cuya base es cuadrada de lado x y las cuatro caras laterales tienen un lado menor igual a: ¼ ò 0.25, (como más te guste), por un lado mayor igual a x.
Mirado la figura donde hay una caja desarrollada, se establece que:
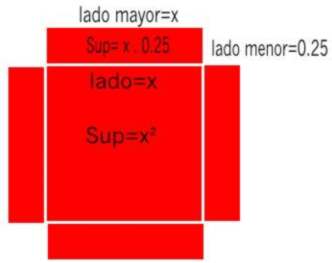
La superficie de la base cuadrada vale lado por lado, es decir: x.x=x²
La superficie de cada cara lateral es: ¼.x=x/4
Como hay 4 caras, la superficie total serà: 4. x/4= x
(Observa que al lado menor lo hace valer 0.25 justamente para que al calcular la superpie de las cuatro caras le dè igual a X,que es el segundo termino de su ecuación.)
Esta superficie vale: 1 (uno) , porque asì dice la ecuación incial.
Es decir: x² + x = 1
Primer miembro superficie caja=Segundo miembro: valor de la superficie=1
Ahora, AL-KHWARIZMI, completa los cuatro cuadraditos de los ángulos, para obtener un nuevo gran cuadrado y calcula la superficie del mismo.

Ahora vale: 1 + la superficie de los 4 nuevos cuadraditos de ¼ de lado.
Por lo tanto la superficie del cuadrado grande es:
1+ 4. 0.25 . 0.25=1.25
Si ahora la superficie del cuadrado vale: 1.25, cuanto vale el lado del mismo?. Hay que buscar un número que multiplicado por sì mismo dè 1.25, y buscado se tiene que es el: 1.118 pues:
1.118 . 1.118=1.25
Y ahora llega el remate final, para obtener el valor de X.
Mira la figura y se observa que si el lado del cuadrado mide 1.118 y los lados de cada cuadradito el de 0.25, cuanto vale ahora X? (que justamente es la raíz de la ecuación).
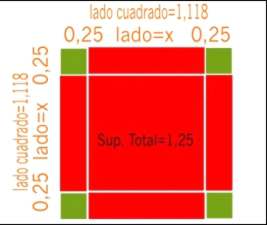
Muy simple debes restar al lado grande, los dos “pedazitos” de los cuadraditos, ósea que: X= 1.118-2. 0.25=0.618...Nota que de esta manera, haciendo una comparación geométrica, este sabio de la alta edad media, pudo llegar a conocer el valor de X.
Aquí se aplicó para obtener el numero de oro de la ecuación planteada a partir de las condiciones de proporcionalidad entre dos segmentos.
Este método es universal, y se puede aplicar a cualquier ecuación que tenga soluciones en el campo real.
Sólo debe estimarse cuanto vale el lado menor de las caras laterales, para que al calcular el área total de las cuatro caras, te dè el valor del segundo término de la ecuación.
Temas Relacionados:
Resolvente de Segundo Grado Online Resolucion Ecuacion
Aplicar la Resolvente Para Ecuaciones de Segundo Grado
Propiedades de las Raices de una Ecuación Cuadratica
Formula del Vértice de una Parabola Cuadrática
Sistema de Ecuaciones Lineales:Resolucion Online
Tartaglia Nicolás:Matemático y su Metodo de Resolver Una Ecuación
Disputas Matemáticas En el Siglo XVI Tartaglia, Cardano y Del Ferro
Enlace Externo:• Método Gráfico para la solución de ecuaciones de segundo






