Teoría Cinética de los Gases Ideales: Modelo Molecular, Resumen
Teoría Cinética de los Gases Ideales: El Modelo Molecular
El comportamiento análogo de todos los gases sugiere que su estructura debe ser la misma.
Como que los gases son muy compresibles, sus moléculas deben estar muy separadas y como que los gases tienden a expandirse hasta ocupar el máximo volumen posible, sus moléculas deben hallarse en un movimiento incesante.
• ►DESCRIPCIÓN BÁSICA:
La teoría cinética de los gases supone que éstos están constituidos por diminutas partículas (moléculas) en constante movimiento.
A igualdad de condiciones, la velocidad promedio con que se mueven las moléculas varía de gas a gas, siendo la regla que cuanto mayor sean las partículas, tanto menor será su velocidad, pero para un gas determinado, la velocidad promedio con que se mueven sus moléculas depende de su temperatura.
Si el gas es calentado, sus moléculas reciben energía para acelerar su movimiento.
La temperatura no es sino una medida de la energía promedio de las moléculas.
Además, estas moléculas son consideradas perfectamente elásticas.
Como están en continuo movimiento, chocan continuamente entre sí y rebotan.
Ahora bien, si dejamos caer al suelo una pelota de goma, rebotará más de una vez, pero con cada rebote se elevará menos del suelo.
En otras palabras, la pelota pierde energía cada vez que da un bote.
Pero las moléculas no pierden ninguna energía cuando chocan entre sí y rebotan.
El movimiento molecular explica el comportamiento de los gases en relación al aumento de temperatura y cambios de presión.
A una cierta temperatura y presión el mismo número de moléculas de cualquier gas ocupa el mismo volumen.
Pero si aumenta la temperatura del gas sus moléculas habrán adquirido la energía necesaria para moverse más rápido.
Chocan más rápido y rebotan más lejos, en otras palabras, ocupan más espacio, pero si no se les permite ocupar mayor espacio, es decir, si el recipiente es rígido, la presión del gas aumentará.
Esto es comprensible, porque la presión del gas sobre las paredes es simplemente la fuerza ejercida por las moléculas que chocan contra ellas.
Si las moléculas aceleran, golpearán las paredes del recipiente con mayor fuerza.
• ►EXPLICACIÓN FÍSICA CONCEPTUAL
 Uno de los fenómenos referentes al comportamiento de los gases que indica el camino más acertado para investigar su naturaleza es el movimiento browniano, observado en 1827 por el escocés Robert Brown y que consiste en una agitación desordenada, en zigzag, ejecutada por las partículas que se hallan en suspensión en los líquidos o en los gases.
Uno de los fenómenos referentes al comportamiento de los gases que indica el camino más acertado para investigar su naturaleza es el movimiento browniano, observado en 1827 por el escocés Robert Brown y que consiste en una agitación desordenada, en zigzag, ejecutada por las partículas que se hallan en suspensión en los líquidos o en los gases.
Cuanto menor es la partícula observada, más claramente se pone de manifiesto su estado de movimiento desordenado permanente y cuanto mayor es la temperatura tanto mayor es la violencia de dicho movimiento.
El movimiento browniano sugiere un estado de continua agitación de las moléculas que constituyen los cuerpos materiales.
Todo parece indicar que la materia está formada por partículas muy pequeñas en movimiento incesante.
Esta teoría de las moléculas en constante agitación se denomina teoría cinética de la materia y sus dos postulados fundamentales son:
a) Las moléculas están en constante movimiento.
b) El calor es una manifestación del movimiento de las moléculas.
APLICANDO ESTOS POSTULADOS A LOS GASES:
Cuando Boyle descubrió en 1661 su sencilla ley experimental sobre el comportamiento de los gases, trató de idear un modelo que interpretara coherentemente la naturaleza del gas.
Ése fue el comienzo de la teoría cinética, desarrollada por Daniel Bernoulli, James Joule, Rudolph Clausius, Ludwig Boltzmann y Albert Einstein, entre otros científicos.
Esta teoría se propone dar una explicación microscópica de las leyes macroscópicas experimentales.
Las hipótesis de las que parte son simples:
1) Un gas consiste en un conglomerado de partículas
(átomos o moléculas) que responden a las leyes de la Mecánica newtoniana. En un gas perfecto pueden despreciarse las fuerzas atractivas entre las moléculas. Así pues, las moléculas pueden considerarse independientes unas de otras.
2) La enorme cantidad de partículas se mueven caóticamente
y están tan separadas entre sí que su propio volumen es despreciable frente al que ocupa todo el gas.
3) No existen fuerzas apreciables sobre las partículas
salvo las que operan durante los choques elásticos entre sí y contra las paredes.
4) En un conjunto de moléculas dado, en un instante determinado,
las moléculas poseen distintas velocidades y, por tanto, sus energías cinéticas también son distintas. Se admite, sin embargo, que la energía cinética media de todas las moléculas es directamente proporcional a la temperatura absoluta del gas.
RESPECTO A LAS MAGNITUDES FÍSICA ES:
• La presión de un gas: lo que llamamos la presión de un gas no es más que el resultado de todo el conjunto de choques que las moléculas efectúan sobre las paredes de un recipiente.
• La temperatura, es según lo dijo Boltzmann: «La temperatura es la medida de la agitación de los átomos». A alta temperatura los átomos se hallan muy agitados y a baja temperatura están más calmados.
EXPLICACIÓN DE LA TEORÍA:
Es razonable que, dado que las partículas están tan separadas, las fuerzas intermoleculares sean solamente las de los choques.
Como los choques son elásticos, entonces se conserva la cantidad de movimiento y también la energía cinética.
Entre choque y choque, las moléculas viajan con movimiento rectilíneo y uniforme, de acuerdo con las leyes de Newton.
Las colisiones son de muy corta duración.
Es decir que la energía cinética se conserva constante, ya que el breve tiempo en que ésta se transforma en energía potencial (durante el choque) se puede despreciar.
A partir de estos supuestos, la teoría explica el comportamiento conocido de los gases y hace predicciones que luego son constatadas experimentalmente, lo que le confiere validez científica.
 Para describir el comportamiento del gas no es imprescindible la historia individual de cada partícula, sino que se recurre a la estadística para interpretar las variables macroscópicas como cierto promedio de propiedades microscópicas.
Para describir el comportamiento del gas no es imprescindible la historia individual de cada partícula, sino que se recurre a la estadística para interpretar las variables macroscópicas como cierto promedio de propiedades microscópicas.
Por ejemplo, la presión se interpreta microscópicamente como el efecto resultante de millones de partículas chocando azarosamente y ejerciendo pequeñas fuerzas irregulares contra las paredes del recipiente.
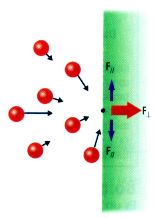
¿Por qué la fuerza que un gas encerrado ejerce sobre la pared del recipiente es perpendicular a su superficie?.
Como todas las posiciones y velocidades son igualmente probables, el bombardeo sobre la pared proviene de todas las direcciones y sentidos.
Las fuerzas ejercidas en dirección paralela a la pared en uno y otro sentido tienden en promedio a anularse.
Pero las fuerzas ejercidas en dirección perpendicular, por el contrario, se sumarán, ya que ninguna partícula colisiona desde el lado exterior de la pared.
La temperatura se interpreta como una medida de la energía cinética media por molécula.
Al calentar un gas, aumentamos la agitación molecular, elevando la velocidad media de las partículas.
Si disminuye la temperatura del gas, se puede licuar.
Es coherente que la energía cinética media de una partícula líquida sea menor que la correspondiente a una partícula gaseosa.
En 1827, el botánico inglés Robert Brown (1773-1858) constató, por primera vez, que partículas pequeñas de materia inerte, suspendidas en un líquido y observadas con un microscopio presentan una agitación azarosa y permanente dependiente de la temperatura.
La explicación de este fenómeno se logró ochenta años después.
El descubrimiento del movimiento browniano permitió un desarrollo posterior más profundo de la teoría cinética.
El movimiento de los gránulos observados a través del microscopio se interpretó como la ampliación del movimiento de las pequeñísimas moléculas invisibles a la lente.
Basándose en un estudio cuantitativo del movimiento browniano, la teoría cinética permite calcular, entre otros múltiples resultados, el número de moléculas contenidas en un volumen dado, a cierta temperatura y presión, para todos y cualquier gas.
DEMOSTRACIÓN DE LA ECUACIÓN DE ESTADO A PARTIR DE LA TEORÍA CINÉTICA DE LOS GASES:
La ecuación de estado de los gases, PV = nRT, puede deducirse de la teoría cinética estudiando el aumento de presión que se produce en un gas a consecuencia de los impactos de las moléculas.
En efecto, consideremos un gas encerrado en una caja.
Su presión es proporcional al número de choques moleculares por segundo sobre cada cm2 de la pared de la caja y proporcional también al impulso mecánico o variación de la cantidad de movimiento de cada impacto.
La presión total será, pues, igual al producto del número de impactos por el impulso mecánico.
El movimiento de cualquier molécula puede ser descompuesto en tres componentes dirigidas según cada una de las tres aristas de la caja, de donde se deduce que el efecto sobre cada una de las paredes es el mismo que si cada tercera parte de las moléculas se moviese perpendicularmente a cada par de caras opuestas.
Así, N/3 moléculas chocarán con una cara determinada de la caja cúbica, siendo N el número total de moléculas contenidas en la caja.
Entre cada dos impactos sucesivos la molécula deberá recorrer en los sentidos de ida y vuelta la longitud de la arista de la caja cúbica, l.
Es decir, la distancia entre dos impactos consecutivos recorrida por la molécula es 2.l.
Como que la velocidad media de las moléculas es V cm/s, el tiempo transcurrido en segundos entre dos choques consecutivos será t = 2.l/V y, por tanto, el número de choques por segundo con la pared del recipiente será V/2.l.
Así pues, podemos concluir que el número de impactos que se producirán sobre una cara de la caja por segundo será de:
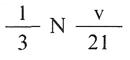
Pero como el área de la cara es l2, el número de impactos por cm2 y por segundo que se producirán será :
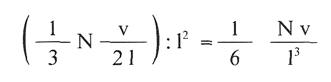
Ahora bien, como el volumen V de la caja es l3, tendremos que el número total de impactos por cm2 y por segundo será:
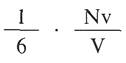
Para obtener el impulso total de cada impacto hay que tener en cuenta que el impulso mecánico es igual a la variación de la cantidad de movimientos.
En toda colisión en la que una molécula de masa m y velocidad v rebote de la pared con igual velocidad absoluta pero en sentido contrario, la cantidad de movimiento variará de un valor inicial mv a un valor final - mv.
Es decir, la variación de la cantidad de movimiento es de 2mv.
Pero tal como se indicó anteriormente, Presión=Fuerza/Área= N° de Impactos/Área . s
Impulso de cada impacto:
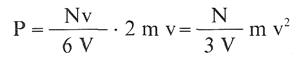
Ahora bien, la energía cinética media de las moléculas y la temperatura absoluta del sistema están relacionadas por la expresión:
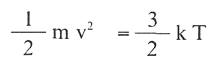
Donde k=1,3805 . 1016 erg./K. molécula es la constante de Boltzmann. Sustituyendo el valor de:
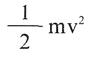
En la ecuación precedente se obtiene:
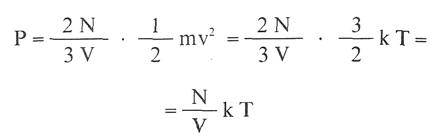
Pero como el número N de moléculas es igual a: 6,023 . 1023 . n , siendo n el número de moles , resulta
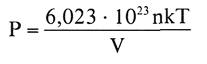
que es la ecuación de estado de los gases ideales,
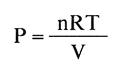
Puede comprobarse sin dificultad que la constante universal de los gases, R, es el producto de la constante k de Boltzmann por el número de Avogadro.
Es decir, R = 6,023 • 1023- k.
RESÚMEN DE LOS POSTULADOS DE LA TEORÍA CINÉTICA DE LOS GASES:

• UN POCO DE HISTORIA...
 Demócrito había dicho que los átomos se hallan en continuo movimiento, agitados de manera desordenada en todos los sentidos.
Demócrito había dicho que los átomos se hallan en continuo movimiento, agitados de manera desordenada en todos los sentidos.
Unas veces, decía, colisionan unos con otros y se pegan como dos bólidos que se dan de frente y se meten uno en otro; otras veces el encuentro termina en una unión que da origen a «sustancias» líquidas o sólidas.
Hacia finales del siglo XIX se descubrió lo esencial de las leyes sobre el comportamiento de los gases, la manera en que se combinan, se mezclan, qué presión ejercen sobre las paredes del recipiente donde se contienen, etc.
Así pues, es natural que en esta época se haya tratado de conocer todas estas propiedades partiendo de la idea de los átomos y de las moléculas que por aquel entonces salía a la luz, es decir, de profundizar en las ideas de Demócrito, pero de una manera un poco más precisa y un poco más cuantitativa.
Si la materia, en este caso el gas, está formada por miles de millones de partículas o de átomos, ¿cómo se pueden explicar, partiendo de sus supuestas propiedades las observaciones de los químicos?.
Dicho de otro modo, ¿cómo a partir de la descripción microscópica de la materia, de las estructuras elementales de las moléculas, se puede construir una teoría que permita explicar propiedades macroscópicas, que son las propiedades con las que trabajan los químicos, desde Gay-Lussac hasta Avogadro pasando por Dalton, hasta llegar a los químicos actuales?.
¿Cómo se puede pasar de las fórmulas químicas al campo del químico que sintetiza nuevos productos? Era menester volver a las fuentes.
Daniel Bernouilli, un genovés miembro de una prestigiosa dinastía científica, abrió el camino a finales del siglo XVIII.
Especialista de esa nueva rama de las Matemáticas llamada cálculo de las probabilidades, Bernouilli comprendió muy pronto que, para estudiar una población de átomos en número muy elevado, la mejor manera de lograrlo era hacer un modelo de su comportamiento de manera estadística y definir de ese modo el comportamiento de un átomo medio.
Pero si es cierto que se le deben a él las primeras ideas en la materia, también es cierto que su trabajo no llegó a un resultado definitivo.
Hacia finales del siglo XIX es cuando se desarrollará realmente la Física estadística, en medio de debates tumultuosos y bastante violentos desde el punto de vista intelectual.
Y ello es así porque esta Física estadística topaba de lleno con dos prejuicios sólidamente enraizados en los espíritus.
Agarrándose al primero, algunos, como ya hemos dicho, se oponían a la idea de átomos y de moléculas so pretexto de que nadie los había visto.
Y otros, apoyados en el segundo, rechazaban la utilización del cálculo de probabilidades.
¿Cómo la naturaleza, decían, cuyas leyes son perfectamente claras y están perfectamente determinadas, podría obedecer al cálculo de probabilidades, al azar, «esa máscara de nuestra ignorancia», como diría más tarde con humor Emile Borel, gran probabilista francés?
Tres hombres, tan distintos como excepcionales, son los que van a construir esta Física estadística.
James Clark Maxwell

Ludwig Boltzmann

Josiah Willard Gibbs

James Clark Maxwell, el autor de la grandiosa teoría de la unificación electromagnética, el gentleman escocés de Cambridge, una de las leyendas de la Física.
El es quien dará la señal de partida calculando la distribución de las velocidades de las partículas de un gas. Maxwell será un gran matemático, pero un atomista desapasionado.
Desgraciadamente morirá en plena batalla en 1918.
Ludwig Boltzmann es un austríaco más joven que Maxwell, a quien admira y venera.
Es un hombre caprichoso, matemático brillante, intelectual-mente ambicioso, con imaginación y con técnica a la vez, pero también es exageradamente impresionable, con frecuencia indeciso (por tres veces aceptará y rechazará después el puesto de profesor en Berlín, donde enseña el gran físico alemán Helmholtz, todo ello en el plazo de dos años), directo —según algunos, demasiado directo— en sus relaciones sociales.
Sin embargo, él será quien pondrá los cimientos.
Josiah Willard Gibbs. Este es un norteamericano.
Fue profesor en la Universidad de Yale. Aunque era reservado y solitario —se cuenta de él que un día, hablando con un colega, se enteró de que los profesores de Yale estaban remunerados, ¡cosa que él ignoraba!— será él quien instalará la Física estadística y hará la síntesis con la Termodinámica.
Es una verdadera pena que Gibbs y Boltzmann no se encontraran jamás, que por dos veces fallara su encuentro.
Porque parece ser que Gibbs fue uno de los pocos contemporáneos que entendía los artículos de Boltzmann, lo que suponía en él una gran experiencia matemática, además de una lucidez introspectiva considerable, dado lo abigarrados y difíciles que eran los artículos de Boltzmann.
Fuente Consultada:
Un Poco de Ciencia Para Todo el Mundo Claude Allégre
Elementos de Física y Qumica Maiztegui-Sabato
Guía de Apoyo Para El Estudiante Tomo: Física.
Temas Relacionados:
Dilatación de los Gases
Los gases nobles Gases Inertes Argon Neon Helio
Los Gases Nobles: Propiedades ,Aplicaciones y Concepto de Gas
Leyes de los Gases Ideales Ley de Boyle, Lussac y Ecuacion
El Humo: Gases de Combustión, Características y Concepto
Gas Natural Clasificación, Distribución, Transporte
Enlace Externo:• Introducción a la teoría cinetica de los gases






